All references are to J. Am.Chem. Soc., 2019, 141.
1. C. S. Anstöter, J. P. Rogers, and J. R. R. Verlet (p. 6132 – 6135) determined the anion-π bond strength of iodide ion with hexafluorobenzene using photoelectron spectroscopy. They find that the anion-π bond strength is 51 kJ/mol. How does this compare to a classical calculation? If there is a significant difference, provide an explanation. For C6F6 the dipole moment is 0 D and the polarizability is 9.58 Å3.
This is an example of a ion-induced dipole interaction:
E = –½×(Z±2α)/(4πεor4)
Z = –1×1.602×10–19 C
α = 9.58 Å3 = 9.58×10–30 m3
4πεo = 1.113×10–10 J–1C2m–1
r = 220 + 312 pm = 5.32×10–10 m
E = –½×(–1.602×10–19 C)2(9.58×10–30 m3) (6.022×1023 mole–)/ (1.113×10–10 J–1C2m–1)(5.32×10–10 m)4
E = 8.3 kJ/mole
The classical values is much smaller than the measured value, indicating that there is a significant contribution to the bonding from other mechanisms, which would include Van der Waal's forces and covalency from orbital overlap. The The other possibility to consider is that the distance estimate is significantly in error. However, to reach the experimental value requires the distance between the iodide ion and the hexafluorobenzene to be 338 pm, which is far too small.
2. G. Yan, T. Wähler, R. Schuster, M. Schwarz, C. Hohner, K. Werner, J. Libuda, and P. Sautet (p. 5623 – 5627) investigated the interaction of water with the surface of Co3O4, which can be used as a heterogeneous redox catalyst. What is the oxidation of the cobalt in this oxide? Given this oxidation state, is it reasonable that oxide can act as a redox catalyst? Why or why not? Surface cobalt ions are in a C3v local environment. Which type of holes does this imply the cobalt ions occupy in the bulk? When the surface is exposed to water, how many water molecules would you expect to bind to each cobalt ion? Explain your reasoning.
The average oxidation state of the cobalt is +8/3, implying a mixture of +2 (one-third of sites) and +3 ions (two-thirds of sites).
The mixed oxidation state means that the energy difference between the +2 and +3 states in the crystal must be quite small, which is ideal for catalysis.
For the surface cobalt ions to exist in a C3v environment there must be 3 nearest neighbors, implying that the cobalt occupies octahedral holes on the crystal side but above surface there is no occupation.
Given that the surface cobalt ions have incomplete coordination and prefer an octahedral environment, it would take three water molecules to complete the coordination sphere.
3. H. Wang, V. C. Jordan, I. A. Ramsay, M. Sojoodi, B. C. Fuchs, K. K. Tanabe, P. Caravan, and E. M. Gale (p. 5916 – 5925) studied a redox active iron complex, shown below, as an MRI contrast reagent (requiring a magnetic moment). Predict the spin-only magnetic moment for the two oxidation states shown in units of Bohr-magnetons. The anion is a poorer contrast agent than the neutral molecule. Is this consistent with your estimates of the magnetic moment? Why or why not?
The coordination around the Fe atom is from three N atoms that are neutral (the lone pairs from the neutral state are the donors), O from water that is neutral (again, one of the lone pairs is the donor), and three O atoms that are from acetate ions. Thus, the ligand has a –3 charge. Then, the complex with 0 charge is Fe3+ and the complex anion is Fe2+.
The amine donors are strong field ligands and the pyridine is a very strong field ligand. Water is a weak field ligand but near the crossover point on the spectrochemical series. The acetate ions are not listed on the given spectrochemical series but should be similar to oxalate ion, which is adjacent to water in terms of ligand field strength. Finally, the complex is seven-coordinate, which will lead to additional electrostatic interactions on the Fe d orbitals, which should increase 10Dq. The net is that the complex is predicted to be low-spin. Thus, for Fe3+, d5, there will be one unpaired spin giving μ = [1(1+2)]½ = 1.73 μB. For Fe2+, d6, there are no unpaired spins so μ = 0 μB.
The predicted magnetic moments are in agreement with the contrast ability. The anion is diamagnetic so causes little contrast in an MRI image while the neutral complex has a magnetic moment, allowing for contrast.
4. N. A. Hirscher, D. P. Sierra, and T. Agapie (p. 6022 – 6029) developed ethylene oligomerization catalysts using chromium complexes. In comparing the complexes shown below, the authors assert that I is too stable for catalysis, III is too reactive, and II is “just right”. What bonding theory best supports their assertions. Explain your reasoning.
These are all organometallic complexes so the first inclination is to use a covalent based theory. Using the EAN rule gives:
I: Cr3+, d3; phenyl anion contribute 2 e–; amine N donates 2 e–; so the total is 3 + 3(2) + 3(2) = 15 e–
II: Cr3+, d3; phenyl anion contribute 2 e–; ether O donates 2 e–; so the total is 3 + 3(2) + 3(2) = 15 e–
III: Cr3+, d3; phenyl anion contribute 2 e–; ether O donates 2 e–; so the total is 3 + 3(2) + 3(2) = 15 e–
All three complexes are 15 e– so distinguishing the reactivity of the three complexes is difficult.
Since Cr3+ is the metal site, a ligand field theory approach is also reasonable:
I: 3 chelating ligands with all 6 donors being strong ligands.
II: 3 chelating ligands with 3 donors being strong ligands and 3 donors being weak ligands (ether O atoms).
III: No chelating ligands with 3 donors being strong ligands and 3 donors being weak ligands (ether O atoms).
In I all of the ligands are strong so substitution at any site will be energetically unfavorable.
In III the three THF ligands are weak and substitution is easily accomplished.
In II the 3 ether O sites are weak but part of a chelate, which will reduce the rate of substitution.
Thus, ligand field theory qualitatively explains the reactivity quite well.
5. S. Tian, J.-F. Zhang, C. Li, T. Ying, S. Li, X. Zhang, K. Liu, and H. Lei (p. 5326 – 5333) measured the magnetic and structural properties of VI3. The structure shows that the vanadium ion is surrounded by six iodides in Oh symmetry. At high temperature the magnetic susceptibility follows the Curie-Weiss law. Predict the room temperature (300 K) magnetic moment and paramagnetic susceptibility. At 50 K there is a sharp increase in the magnetic susceptibility and at 2 K the magnetic susceptibility is strongly hysteretic. Explain what happens to the magnetic properties below 50 K.
V3+ is d2 so μ = [2(2+2)]½ = 2.83 μB
μeff = 2.828(χparaT)½ so χpara = (μeff/2.828)2/T = (2.83/2.828)2/300 = 3.34×10–3
The hysteresis at 2 K implies ferromagnetic or antiferromagnetic behavior. The increase in susceptibility at 50 K can only happen for ferromagnetism. Thus, the compound is paramagnetic above 50 K and there is a phase transition to being ferromagnetic at 50 K and below.
6. Z. Wu, C. Chen, J. Lie, Y. Lu, J. Xu, X. Liu, G. Cui, T. Trabelsi, J. S. Francisco, A. Mardyukov, A. K. Eckhardt, P. R. Scheiner, and X. Zeng (p. 3361 – 3365) followed the photolytic decomposition of S-nitrosothiols, H3CSNO. Draw the Lewis dot structure for this compound and predict all of the bond angles.
Lewis structure: 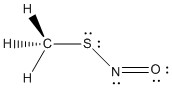
H-C-H bond angles: ~109°
H-C-S bond angles: ~109°
C-S-N bond angle: ~107°
S-N-O bond angle: ~118°
7. J. J. Moreno, M. F. Espada, J. Campos, J. López-Serrano, S. A. Macgregor, and E. Carmona (p. 2205 – 2210) used (η5-C5Me5)(PMe2Ar)Ir(III), shown below, to activate C-H bonds. How must the phenyl ring shown in red be bonded to the Ir for the complex to be stable?
Use the EAN rule to answer the question: Ir3+ is d6, the C5Me5 donates 6 e–, and the substituted P atom donates 2 e–. This totals to 6 + 6 + 2 = 14 e–. To be stable the metal center prefers 18 e–. To reach this total two of the double bonds in the phenyl ring must donate, which means the phenyl ring is η4. (η2 bonding, one double bond, would lead to a 16 e– complex, which might also be stable.)
8. S. Kundu, P. N. Phu, P. Ghosh, S. A. Kozimor, J. A. Bertke, S. C. E. Stieber, and T. H. Warren (p. 1415 – 1419) examined linkage isomerization in the nickel β-diketiminato complex shown below. The visible spectrum of the complex showed a single peak at 615 nm with ε = 150 M–1cm–1. What is the oxidation state of the nickel? Is this consistent with the visible spectrum? Why of why not? What is the value for 10Dq (in units of cm–1)?
The β-diketiminato ligand is monoanionic and the NO ligand is neutral, thus the nickel is in the +1 oxidation state.
Ni+ is d9, which has a single allowed d-d transition in Oh with a molar absorptivity of 100 M–1cm–1 or less. This is in agreement with the observed single absorption and since this complex is only 3-coordinate a slightly higher absorption coefficient is expected.
For d9 complexes the single peak is at 10Dq so ν = 615 nm = 16300 cm–1 = 10Dq.
9. E. Hayashi, Y. Yamaguchi, K. Kamata, N. Tsunoda, Y. Kumagai, F. Oba, and M. Hara (p. 890 – 900) found that the crystal structure of MnO2 affected the catalytic activity for oxidation. In the β-phase the crystal structure is approximately the same as fluorite (where the cation is 4-coordinate, the anion is 8-coordinate, and M = 2.519) while the γ-phase is approximately the same as the rutile structure (where the cation is 6-coordinate, the anion is 3-coordinate, and M = 2.408). Estimate the lattice energy for each phase in units of kJ/mole. For one example oxidation the ratio of the catalysis is 28/5 for β-phase to γ-phase. Is the difference accounted for by the difference in lattice energy? Why or why not?
Use either the Born-Mayer or Kapustinskii equation to answer the question. Without a way to estimate the Born exponent, the Born-Landé equation is not useful.
For the β-phase ro = 37 + 142 = 179 pm
For the γ-phase ro = 53 + 137 = 190 pm (A value for 3-coordinate oxide is estimated to be slightly less than 4-coordinate.)
Kapustinskii:
β-phase: Elatt = –1202(3)(+4)(–2)(1 – 0.345/1.79)/1.79 = 13000 kJ/mol
γ-phase: Elatt = –1202(3)(+4)(–2)(1 – 0.345/1.90)/1.90 = 12400 kJ/mol
Born-Mayer:
β-phase: E = –(6.022×1023)(2.519)(+4)(–2)(1.602×10–19)2 (1 – 34.5/179)/(1.113×10–10)(1.79×10–10) = 12600 kJ/mol
γ-phase: E = –(6.022×1023)(2.408)(+4)(–2)(1.602×10–19)2 (1 – 34.5/190)/(1.113×10–10)(1.90×10–10) = 11500 kJ/mol
Depending on which calculation, the γ-phase has 4 to 9 % smaller lattice energy. This is not enough difference to account for the more than five-fold difference in reactivity. This is to be expected: catalysis occurs at surface sites, not in the bulk so the lattice energy should have, at best, a very small influence on catalytic behavior.