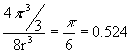
There is 1 sphere per unit cell (8 corners × 1/8 = 1) with a volume of 4πr3/3. The length of the unit cell a = 2r (since the spheres are assumed to be touching) so the volume of the cell is (2r)3 = 8r3. The fraction of filled space is
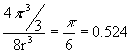
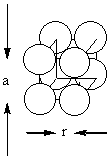
A sketch of the unit cell is shown below:

There is 1 sphere per unit cell (8 corners × 1/8 = 1) with a
volume of 4πr3/3. The length of the
unit cell a = 2r (since the spheres are assumed to be touching) so the
volume of the cell is (2r)3 = 8r3. The fraction of
filled space is