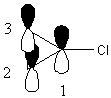
The molecule belongs to the C2v point group. Use the p orbitals perpendicular to the page as the basis set. The z axis is along the C-Cl bond and let the x axis be in the plane of the paper. Let p1 be on the C connected to Cl and number clockwise around the ring.
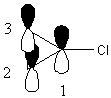
| C2v |
|
|
|
|
| a1 |
|
|
|
|
| a2 |
|
|
|
|
| b1 |
|
|
|
|
| b2 |
|
|
|
|
| p orbitals |
|
|
|
|
| R(p1) |
|
|
|
|
| R(p2) |
|
|
|
|
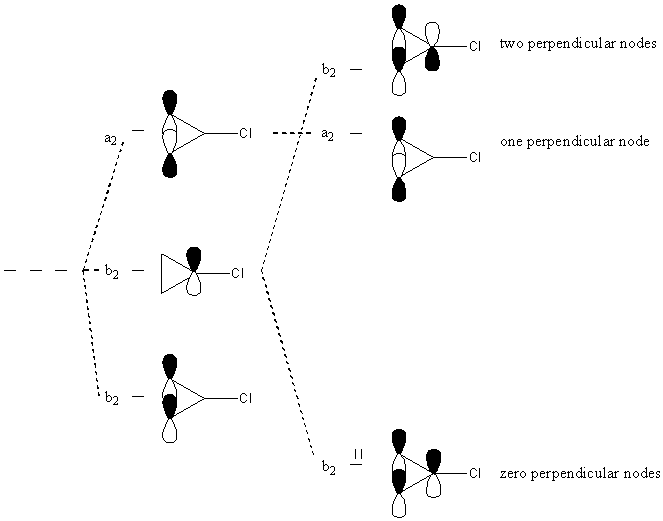
n(a1) = [(1)(1)(3) + (1)(1)(–1) + (1)(1)(–3) + (1)(1)(1)]/4 = 0
n(a2) = [(1)(1)(3) + (1)(1)(–1) + (1)(–1)(–3) + (1)(–1)(1)]/4 = 1
n(b1) = [(1)(1)(3) + (1)(–1)(–1) + (1)(1)(–3) + (1)(–1)(1)]/4 = 0
n(b2) = [(1)(1)(3) + (1)(–1)(–1) + (1)(–1)(–3) + (1)(1)(1)]/4 = 2
a2 + 2b2
From the results of the symmetry operations on each orbital, p1 is never changed with any other orbital, so its representation is found by simply inspecting the characters (1, –1, –1, 1) and is one of the b2 orbitals.
Using the projection operators gives:
P(a2 p2) = (1)p2 + (1)(–p3) + (–1)(–p2) + (–1)(p3) = 2[p2 – p3]
Ψ(a2) = 2½[p2 – p3]
P(b2 p2) = (1)p2 + (–1)(–p3) + (–1)(–p2) + (1)(p3) = 2[p2 + p3]
Ψ(b2) = 2½[p2 + p3]