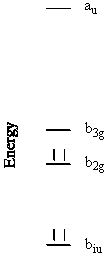
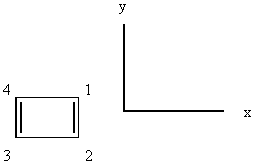
1. Cyclobutadiene, shown below, is an antiaromatic molecule (that is, the π electrons do not delocalize around the ring). In this problem you will construct the molecular orbital diagram for the π system by considering each π orbital as a group orbital on the carbon atoms. Use the axis system shown (z is perpendicular to the page) and the p_z orbitals on each carbon atom as the basis set. Find the irreducible representations of the π orbitals. Use the projection operator technique to find the wavefunctions of each of the π orbitals. Sketch each of these orbitals. Energy order the orbitals and show the electron occupation in your MO diagram.

Number the C atoms. Cyclobutadiene belongs to the D_2h point group:
 

D2h	E	C2(z)	C2(y)	C2(x)	i	σ(xy)	σ(xz)	σ(yz)
ag	1	1	1	1	1	1	1	1		x2, y2, z2
b1g	1	1	-1	-1	1	1	-1	-1	Rz	xy
b2g	1	-1	1	-1	1	-1	1	-1	Ry	xz
b3g	1	-1	-1	1	1	-1	-1	1	Rx	yz
au	1	1	1	1	-1	-1	-1	-1
b1u	1	1	-1	-1	-1	-1	1	1	z
b2u	1	-1	1	-1	-1	1	-1	1	y
b3u	1	-1	-1	1	-1	1	1	-1	x

Total representation for the π orbitals:

	E	C2(z)	C2(y)	C2(x)	i	σ(xy)	σ(xz)	σ(yz)
pz	4	0	0	0	0	-4	0	0

This reduces to b_2g + b_3g + a_u + b_1u

Rotation operator:
 

	E	C2(z)	C2(y)	C2(x)	i	σ(xy)	σ(xz)	σ(yz)
Rp1z	p1z	p3z	-p4z	-p2z	-p3z	-p1z	p2z	p4z

Projection operator:

P(b_2g) = p_1z - p_3z - p_4z + p_2z - p_3z + p_1z + p_2z - p_4z

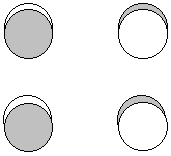
1 node between the sigma (long) bonds
 
 

P(b_3g) = p_1z - p_3z + p_4z - p_2z - p_3z + p_1z - p_2z + p_4z

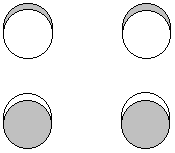
1 node between the pi (short) bonds
 

P(a_u) = p_1z + p_3z - p_4z - p_2z + p_3z + p_1z - p_2z - p_4z

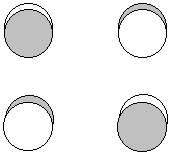
2 nodes
 

P(b_1u) = p_1z + p_3z + p_4z + p_2z + p_3z + p_1z + p_2z + p_4z

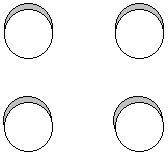
0 nodes
 

Energy Level Diagram: