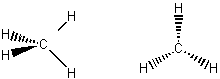
Orbitals are treated as objects that can be labeled by their irreducible representations
This can be done within either the VBT or LCAO-MO approaches
Find the irreducible reps of the bond pairs; this allows us to label the bonds into different energy groups but gives no indication of the relative energy of each type of irred. rep.
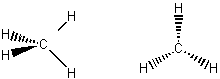
| Td |
|
|
|
|
|
||
| a1 |
|
|
|
|
|
|
|
| a2 |
|
|
|
|
|
||
| e |
|
|
|
|
|
|
|
| t1 |
|
|
|
|
|
|
|
| t2 |
|
|
|
|
|
|
|
| σ bonds |
|
|
|
|
|
These transform as a1 + t2
a1 is also an s orbital; t2 is also px, py, pz orbitals which implies an sp3 hybrid
find irred reps of bonds; find hybrid
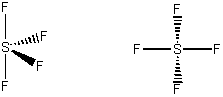
| C2v |
|
|
|
|
||
| a1 |
|
|
|
|
|
|
| a2 |
|
|
|
|
|
|
| b1 |
|
|
|
|
|
|
| b2 |
|
|
|
|
|
|
| bonds |
|
|
|
|
||
| lp |
|
|
|
|
bonds 2a1 + b1 + b2 sp3
hybrid?
lp transforms as a1 therefore dsp3 hybrid!
attempt to use symmetry to convert polyatomic problems into something like a diatomic problem.
1. Break the molecule up into two parts: the center atom and all the atoms bonded to it.
2. Find the irreducible representations of the basis orbitals on the center atom, generally by inspection of the character table.
3. Create "Group Orbitals" from the basis orbitals on the peripheral atoms using symmetry operations.
4. Estimate overlaps remembering that only orbitals of the same irreducible rep can overlap with each other.
| C2v |
|
|
|
|
||
| a1 |
|
|
|
|
|
|
| a2 |
|
|
|
|
|
|
| b1 |
|
|
|
|
|
|
| b2 |
|
|
|
|
|
|
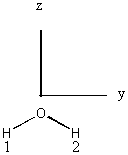
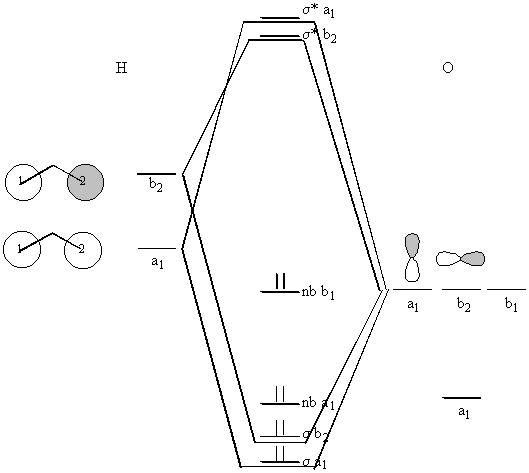
Basis set: H, 1s; O 2s, 2p
Irreducible reps of the O basis orbitals are read directly from the character table:
2s – a1
2pz – a1
2px – b1
2py – b2
The irreducible reps of the H orbitals must be done as a group since they are not located at the "center" of the molecule.
Reducible rep of H 1s orbitals:
| E | C2 | σv(xz) | σv'(yz) | |
| 1s Group | 2 | 0 | 0 | 2 |
This total rep transforms as a1 + b2
What do the a1 and b2 group orbitals look like?
Use projection operators:
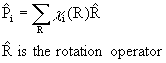
Note that the sum is over all rotations, not just classes!
Use the rotation operator on the H s orbitals:
| E | C2 | σv(xz) | σv'(yz) | |
| s1 | s2 | s2 | s1 |
Since s1 and s2 are connected by symmetry, we do not need to use the rotation operator on s2.
Now, use the projection operator for each group orbital:
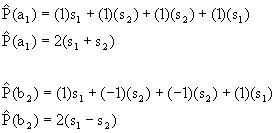
The wavefunctions are the result of the projection operator normalized:
Ψ(a1) = 2N(s1+s2), where N is the normalization constant.
Normalized wavefunctions are found by squaring the function and setting it equal to 1:
Ψ2 = 1 = 4N2(s1+s2)2
s12 = s22 = 1; s1s2
= 0, so ![]()
![]()
Likewise
![]()
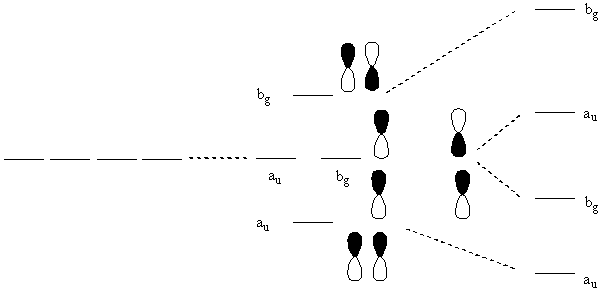
Consider all trans butadiene. Find the relative orbital energies of the π orbitals and label them with their irreducible representations.
![]()
Point Group: C2h
| C2h |
|
|
|
|
||
| ag |
|
|
|
|
Rz | x2, y2, z2, xy |
| bg |
|
|
|
|
Rx, Ry | xz, yz |
| au |
|
|
|
|
z | |
| bu |
|
|
|
|
x, y |
Find the transformation properties of the p orbitals that form the π orbitals:
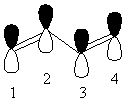
|
|
|
|
|
|
| p orbitals |
|
|
|
|
This gives 2bg + 2au
Now use projection operators to find the composition of each molecular orbital:
|
|
|
|
|
|
| p1 |
|
|
|
|
| p2 |
|
|
|
|
P(bg-1) = [(1)p1 + (–1)p4 + (1)(–p4) + (–1)(–p1)] = 2(p1 – p4)
Ψ(bg-1) = 2–½(p1–p4)
P(bg-2) = [(1)p2 + (–1)p3 + (1)(–p3) + (–1)(–p2)] = 2(p2 – p3)
Ψ(bg-2) = 2–½(p2 – p3)
P(au-1) = [(1)p1 + (1)p4 + (–1)(–p4) + (–1)(–p1)] = 2(p1 + p4)
Ψ(au-1) = 2–½(p1 + p4)
P(au-2) = [(1)p2 + (1)p3 + (–1)(–p3) + (–1)(–p2)] = 2(p2 + p3)
Ψ(au-2) = 2–½(p2 + p3)
Now draw the MO diagram