Symmetry is associated with the idea that certain geometrical transformations leave an object unchanged. The geometric operations that do this for molecules are called symmetry elements or symmetry operations. The set of all symmetry elements associated with a molecule obeys the properties associated with a mathematical group so the mathematics of group theory can be applied to molecules. This math allows us to characterize and label some properties of molecules such as molecular orbitals or spectroscopic transitions. In this course, we will use group theory to label molecular orbitals, which will be used to construct molecular orbital diagrams and understand bonding in molecules.
There are 4 classes of symmetry elements:
1. Inversions
2. Rotations1. + 2. lead to Point Groups
3. Translations1. + 2. + 3. lead to Space Groups
4. Time Inversions1. + 2. + 3. + 4. lead to Magnetic Space Groups
1. Inversion i
The signs of the Cartesian coordinates are made negative leaving the object invariant in appearance (absolutely identical)
2. Rotations Cn
An angular motion of 360°/n clockwise (by convention) about an axis (the axis may be defined in the symmetry element)
special cases: 0o rotation is given the symbol E and acts as the identity element in group theory
C∞ is an infinitely small rotation - appropriate for linear molecules
For any given Cn operation, there are n-1 different rotations Cn, Cn2, Cn3, ..., Cnn-1
3. mirrors or planes of symmetry σ
Reflection through a plane that leaves an object invariant
All mirrors are composite symmetry elements - combinations of i and C2
σxy = i×C2z
σv = mirror containing bonds (usually)
σd = mirror between bonds (usually)
σh = mirror perpendicular to highest rotation axis
4. Improper rotations Sn
A rotation followed by a mirror perpendicular to the rotation: Sn = Cn×σh
Note that S2 = i and S1 = σ
The set of all symmetry elements associated with a molecule is called the point group.
Each point group can be generated from a smaller set of symmetry operations known as generators; we only need to be able to identify the generators in order to identify the point group. Knowing the point group is essential to using group theory but also is an indicator of molecular structure!
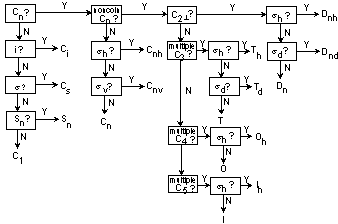
Summary flow chart for finding Point Groups:
