Ligand Field Theory

A better treatment of the bonding in transition metal complexes needs to add a quantum mechanics component and to treat electronic states rather than just a one-electron approach.

Starting with the atomic d orbitals, we know that they split into a number of states simply based on the occupation of the electrons in the different orbitals. We denote these using Term Symbols. The different terms have different energies because of e^––e^– repulsion.

The energies of the different states can be calculated using standard quantum mechanical techniques. In general, the energy of each Term can be expressed as a sum of integrals. Depending on how the linear combinations are expressed, these integrals are expressed as Condon-Shortley parameters (F_o, F₂, F₄) or Racah parameters (A, B, C). Inorganic chemists typically use Racah parameters. For each electron configuration and Term, there is a different linear combination A, B, and/or C that expresses the energy of that state.

From G. Racah, Phys. Rev., 1962, 62, 438.

electron configurationTermRepulsion Energy

d², d⁸

³FA – 8B

 

³PA + 7B

 

¹GA + 4B + 2C

 

¹DA – 3B + 2C

 

¹SA + 14B + 7C

 

d³, d⁷

⁴F3A – 15B

 

⁴P3A

 

²H3A – 6B + 3C

 

²G3A – 11B + 3C

 

²F3A + 9B + 3C

 

²D (2 states)3A + 5B + 5C ± (193B² + 8BC + 4C²)^½

 

²P3A – 6B + 3C

 

d⁴, d⁶

⁵D6A – 21B

 

³H6A – 17B + 4C

 

³G6A – 12B + 4C

 

³F (2 states)6A – 5B + 11C/2 ± (3/2)(68B² + 4BC + C²)^½

 

³P (2 states)6A – 5B + 11C/2 ± ½(912B² – 24BC + 9C²)^½

 

³D6A – 5B + 4C

 

¹I6A – 15B + 6C

 

¹G (2 states)6A – 5B + 15C/2 ± ½(708B² – 12BC + 9C²)^½

 

¹F6A + 6C

 

¹D (2 states)6A + 9B + 15C/2 ± (3/2)(144B² + 8BC + C²)^½

 

d⁵

⁶S10A – 35B

 

⁴G10A – 25B + 5C

 

⁴F10A – 13B + 7C

 

⁴D10A – 18B + 5C

 

⁴P10A – 28B + 7C

 

²I10A – 24B + 8C

 

²H10A – 22B + 10C

 

²G10A – 13B + 8C

 

²G'10A + 3B + 10C

 

²F10A – 9B + 8C

 

²F'10A – 25B + 10C

 

²D (2 states)10A – 3B + 11C ± 3(57B² + 2BC + C²)^½

 

²D'10A – 4B + 10C

 

²P10A + 20B + 10C

 

²S10A – 3B + 8C

 

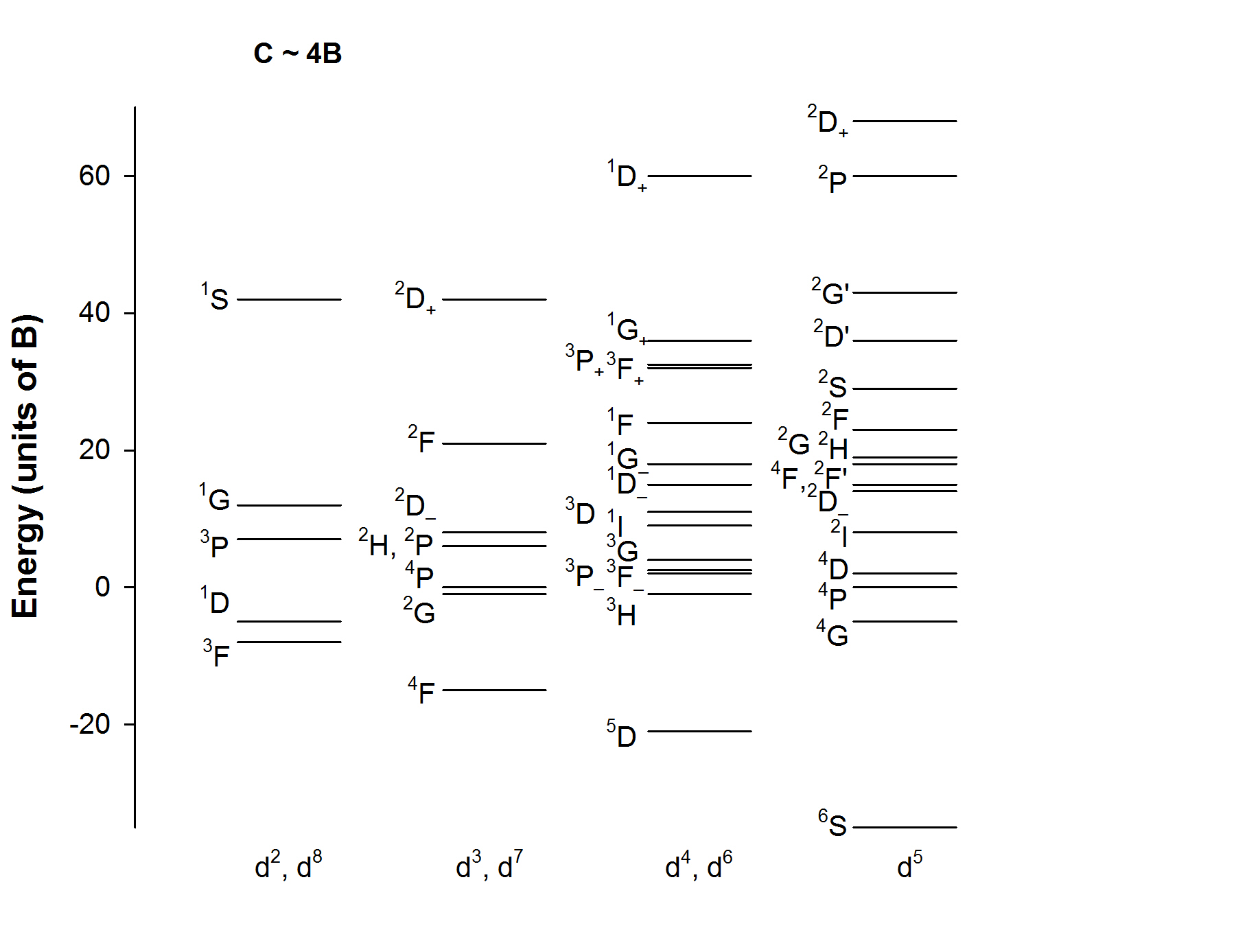
Note that for each electron configuration the repulsion associated with A is constant within all of the energy levels for that electron configuration. Consequently, this term is typically ignored or considered the zero of energy.

Typically, C ~ 4B. Under this assumption, the energy levels for each electron configuration are approximately shown below.

The B parameter varies depending on the ligand and can be measured in many cases. Like the spectrochemical series, the changes in B is largely independent of the metal ion and depends mostly on the bonding of the ligand. B is always reduced from the free ion value because some electron density is moved from the metal to the ligand, which reduces electron-electron repulsion. The reduction of B caused by bonding is called the nephelauxetic effect.

The nephelauxetic parameter is defined as β = B(complex)/B(free ion). The smaller β is the more covalency in the metal-ligand bond.

In the presence of an octahedral field, most of these states splits into two or more states, which can be determined and labeled using group theory in the O_h point group.

For each free electron state. the characters of the O point group (a subgroup of O_h known as a rotation group because the group only contains rotation symmetry elements) are found using the formula Χ(θ) = sin[(L + ½)θ]/sin[θ/2] where L = the orbital angular momentum quantum number associated with the state (L = 0 for S, L = 1 for P, etc.) and θ is the rotation angle for the symmetry angle, and θ ≠ 0. For the E symmetry element, Χ(E) = 2L + 1, the orbital degeneracy of the state.

In O_h the representation determined by the character of the i symmetry element for the type of orbital being considered, i.e. +1 for s, d,and g orbitals and –1 for p and f orbitals. For Χ(i) = +1, the subscript is "g" (gerade) and for Χ(i = –1 the subscript is "u" (ungerade).

Using this method, for the d orbitals the results are:

Free Electron StateState in O_h

SA_1g

PT_1g

DT_2g + E_g

FA_2g + T_1g + T_2g

GA_1g + E_g + T_1g + T_2g

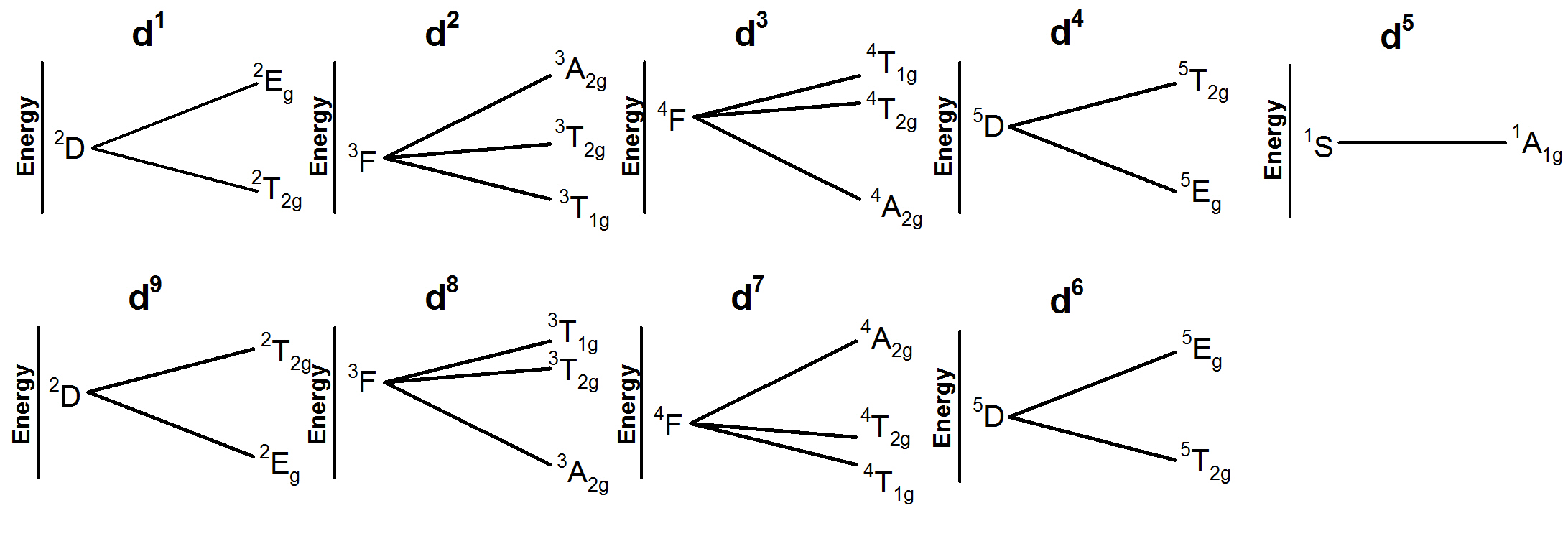
For the ground state free electron states, in a weak O_h field causes the energy level to split:

d¹, d⁹²D → ²E_g + ²T_2g

d², d⁸³F → ³A_2g + ³T_1g + ³T_2g

d³, d⁷⁴F → ⁴A_2g + ⁴T_1g + ⁴T_2g

d⁴, d⁶⁵D → ⁵E_g + ⁵T_2g

d⁵⁶S → ⁶A_1g

The splitting of the lowest energy levels in a weak field are shown below. When all of the same spin degeneracy states are included these are known as Orgel diagrams.

Similar splitting occurs in excited states, which can be labeled using group theory.

In a strong field the relative energies can be found by using the electron configurations.

d¹E(t_2g¹) = –4Dq;   E(e_g¹) = 6Dq

d²E(t_2g²) = –8Dq;   E(t_2g¹e_g¹) = 2Dq   E(e_g²) = 12Dq

d³E(t_2g³) = –12Dq;   E(t_2g²e_g¹) = –2Dq   E(t_2g¹e_g²) = 8Dq   E(e_g³) = 18Dq

d⁴E(t_2g⁴) = –16Dq;   E(t_2g³e_g¹) = –6Dq   E(t_2g²e_g²) = 4Dq   E(t_2g¹e_g³) = 14Dq   E(e_g⁴) = 24Dq

d⁵E(t_2g⁵) = –20Dq;   E(t_2g⁴e_g¹) = –10Dq   E(t_2g³e_g²) = 0Dq   E(t_2g²e_g³) = 10Dq   E(t_2g¹e_g⁴) = 20Dq

d⁶E(t_2g⁶) = –24Dq;   E(t_2g⁵e_g¹) = –14Dq   E(t_2g⁴e_g²) = –4Dq   E(t_2g³e_g³) = 6Dq   E(t_2g²e_g⁴) = 16Dq

d⁷E(t_2g⁶e_g¹) = –18Dq   E(t_2g⁵e_g²) = –8Dq   E(t_2g⁴e_g³) = 2Dq   E(t_2g³e_g⁴) = 12Dq

d⁸E(t_2g⁶e_g²) = –12Dq   E(t_2g⁵e_g³) = –2Dq   E(t_2g⁴e_g⁴) = 8Dq

d⁹E(t_2g⁶e_g³) = –6Dq   E(t_2g⁵e_g⁴) = 4Dq

Further splitting of energy levels occurs when the symmetry is lower than O_h. Again, group theory allows us to label states using Correlation Tables.

Point Group	Oh	O	Td	D4h	D2d	C4v	C2v	D3d	D3	C2h
Irreducible Representation	a1g	a1	a1	a1g	a1	a1	a1	a1g	a1	ag
	a2g	a2	a2	b1g	b1	b1	a2	a2g	a2	bg
	eg	e	e	a1g + b1g	a1 + b1	a1 + b1	a1 + a2	eg	e	ag + bg
	t1g	t1	t1	a2g + eg	a2 + e	a2 + e	a2 + b1 + b2	a2g + eg	a2 + e	ag + 2bg
	t2g	t2	t2	b2g + eg	b2 + e	a2 + e	a1 + b1 + b2	a1g + eg	a1 + e	2ag + bg
	a1u	a1	a2	a1u	b1	a2	a2	a1u	a1	au
	a2u	a2	a1	b1u	a1	b2	a1	a2u	a2	bu
	eu	e	e	a1u + b1u	a1 + b1	a2 + b2	a1 + a2	eu	e	au + bu
	t1u	t1	t2	a2u + eu	b2 + e	a1 + e	a1 + b1 + b2	a2u + eu	a2 + e	au + 2bu
	t2u	t2	t1	b2u + eu	a2 + e	b1 + e	a2 + b1 + b2	a1u + eu	a1 + e	2au + bu

Once the point group is identified, the splitting of the states can be written easily using the correlation table. The energies of the states can not be established using group theory.

A simple example: d¹

The free ion is ²D that splits into ²T_2g (ground state) and ²E_g states. Since the ²T_2g state is triply degenerate, it must further split (Jahn-Teller effect) to remove the degeneracy. Lowering the symmetry to D_4h (by compression of the ligands along the z-axis) the energy states become ²T_2g → ²B_2g (ground state) + ²E_g and ²E_g → ²A_1g + ²B_1g

Another example: What are the fourteen lowest energy states for [Cr(NH₃)₅Cl]²⁺

[Cr(NH₃)₅Cl]²⁺ is a d³ complex with C_4v symmetry. Thus, the energy level diagram is: