An ionic approach to understanding bonding in transition metal complexes
Assumptions
Metal ions are treated as point charges
Ligands are treated as point charges or point dipoles
d orbitals on the metal are considered but ligand orbitals are ignored
The electrostatics of the metal and ligands creates an electric field, denoted V, that is treated as a perturbation in the Hamiltonian describing the energies of the d electrons.
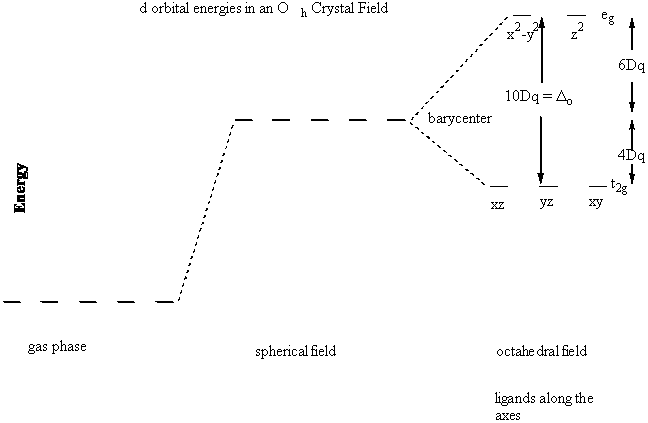
In the case of a gas phase, octahedral complex V = Vsphere + Voct
Vsphere raises the energies of all the d orbitals the same amount, essentially resetting the "zero" of energy
The math is messy, but the solution of the perturbation equation gives two factors that are the same for all of the d electrons:
D = 35Ze2/4(4πεo)a4
q = 2<r4>/105
so that Dq = [1/6][Ze2<r4>/4πεoa5]
where Z is the charge on the metal ion (+1, +2, etc)
e is the charge on the electron = 1.602×10–19 C
r is the distance of the d electron from the metal nucleus; <r4> indicates the average of the distance to the fourth power
a is the distance between the metal and the ligand
εo is the permittivity of free space; 4πεo = 1.113×10–10 J–1C2m–1
Solving for each individual d orbital gives:
E(dz2) = E(x2–y2) = +6Dq
E(dxy) = E(xz) = E(yz) = –4Dq
Graphically:

Δo = 10Dq = Crystal Field Splitting
Order of magnitude of 10Dq:
For Z = +2, r = 1 Å, and a = 2 Å, 10Dq ~ 145 kJ/mol, i.e. this is on the order of weak covalent bond energies
Occupation of the t2g orbitals gives a little extra stabilization of the complex
Ligand Field Stabilization Energy (LFSE)
d electron configurationOh Field configuration LFSEunpaired spins
d1t2g1 4Dq1
d2t2g2 8Dq2
d3t2g3 12Dq3
d4t2g4 16Dq – P2 (low spin)
d4t2g3eg1 6Dq4 (high spin)
d5t2g5 20Dq – 2P1 (ls)
d5t2g3eg2 0Dq5 (hs)
d6t2g6 24Dq – 2P0 (ls)
d6t2g4eg2 4Dq4 (hs)
d7t2g6eg1 18Dq – P1 (ls)
d7t2g5eg2 8Dq3 (hs)
d8t2g6eg2 12Dq2
d9t2g6eg3 6Dq1
d10t2g6eg4 0Dq0
P = spin pairing energy : this energy is not included for any required spin pairing
hs = high spin
ls = low spin
The number of energy levels and degeneracies for any given geometry can be readily obtained using group theory.
The transformation properties of the d orbitals gives the irreducible representations, which will each be of a different energy.
In the case of an Oh complex, the d orbitals transform as t2g + eg, which are easily identified by looking at the quadratic basis functions on the far right of the character table.
Oh Character Table
Oh
E
8C3
6C2
6C4
3C2(=C42)
i
6S4
8S6
3σh
3σd
a1g
1
1
1
1
1
1
1
1
1
1
x2+y2+z2
a2g
1
1
–1
–1
1
1
–1
1
1
–1
eg
2
–1
0
0
2
2
0
–1
2
0
(2z2–x2–y2, x2–y2)
t1g
3
0
–1
1
–1
3
1
0
–1
–1
(Rx,Ry,Rz)
t2g
3
0
1
–1
–1
3
–1
0
–1
1
(xy,yz,xz)
a1u
1
1
1
1
1
1–
–1
–1
–1
–1
a2u
1
1
–1
–1
1
–1
1
–1
–1
1
eu
2
–1
0
0
2
–2
0
1
–2
0
t1u
3
0
–1
1
–1
–3
–1
0
1
1
(x,y,z)
t2u
3
0
1
–1
–1
–3
1
0
1
–1
This makes it easy to identify orbital degeneracy for any geometry. Group theory does not indicate the energy order.
Labeling the orbitals: when the symmetry drops below Oh labeling the d orbitals as t2g and eg is no longer appropriate or correct. Identifying the correct point group and then using the corresponding character table quickly gives the correct irreducible representations to label the orbitals.
A second way to do this is to use a Correlation Table, which shows the connection between the labels of various point groups.
Point Group:
Oh
D4h
C4v
D2d
D3
Td
Irreducible Representation:
eg
a1g + b1g
a1 + b1
a1 + b1
e
e
Irreducible Representation:
t2g
b2g + eg
b2 + e
b2 + e
a1 + e
t1
Group theory does not give us the relative energies of the orbitals, however.
Consider a tetragonal case:
Need to introduce additional parameters, δ1 and δ2
The situation is such that E(dx2–y2) – E(dxy) = 10Dq (moving the ligand along the z axis should have no effect on the relative energies of the orbitals in the xy plane).
For compression case :
[E(dx2–y2) + δ2] – [E(dxy) + 2δ1] = 10Dq
[E(dx2–y2) – E(dxy)] + δ2 – 2δ1 = 10Dq
10Dq + δ2 – 2δ1 = 10 Dq
δ2 = 2δ1
Can we predict when this will happen? Yes, using the Jahn-Teller theorem
Jahn-Teller Theorem: In a nonlinear molecule a degenerate electronic state will distort to remove the degeneracy and to increase the stability
Consider d1
In an Oh geometry, the electronic state is triply degenerate (the single electron can be in one of three orbitals of identical energy).
Axial elongation gives a state that is still degenerate (doubly) so would need to further distort.
Axial compression leads to a singly degenerate state and increased stability.
LFSE = –4Dq – 2δ1
This should occur even if all the ligands are the same!
Which configurations should be J-T active?
configuration
active?
distortion geometry
d1
yes
compression
d2
yes
elongation
d3
no
d4 (hs)
yes
either
d4 (ls)
yes
compression
d5 (hs)
no
d5 (ls)
yes
elongation
d6 (hs)
yes
compression
d6 (ls)
no
d7 (hs)
yes
elongation
d7 (ls)
yes
either
d8
no
d9
yes
either, (nearly always is elongation, often to CN = 4)
d10
no
Tetrahedral symmetry is fairly common but can not be treated as a distortion from Oh
Ligands between axes are destabilized, ligands along axes are stabilized.
The splitting in Td complexes is always less than the splitting in Oh complexes with the same ligands (Δt < Δo). (Fewer ligands give a smaller electrostatic field; in the exact ionic limit Δt = 4Δo/9.)
This means that Td complexes are always high spin and usually bluer.
metal : charge, size (Z*)
ligands : charge, orbitals available for bonding (σ, π), ring formation
Using formation constants for a given ligand and changing metals, it was found that the trend in reactivity is generally the same, independent of the ligand.
This is known as the Irving-Williams series:
Ba2+ < Sr2+ < Ca2+ < Mg2+ < Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+
ligands ordered by relative size of Dq for any metal ion ligands ordered by ligand field strength
I– < Br– < S2– < SCN– < Cl– < NO3– < F – < ox2– < H2O < SCN– < CH3CN < NH3 < en < bipy < phen < NO2– < PPh3 < CN– < CO