Ionic Compounds

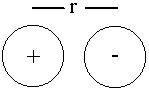
Properties: hard, brittle, high mp and bp, often water soluble, electrolytes in solution or melt, usually crystalline. All of this suggests large bond energies.

Necessary conditions for an ionic compound: cation (implies neutral species has a low ionization energy) and anion (implies neutral has a high electron affinity)

We develop a theory of ionic bonding using simple electrostatics. Assume that the ions behave as point charges (i.e., the ions have no volume). Then build a lattice from condensation of gas phase ions and use Coulomb's law to calculate the energy.

Ion Pair

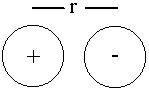
E_dip = q₊q_–/4πε_or

q₊, q_- are the ionic charges in coulombs

r is the distance between ions in meters

ε_o is the permittivity of free space

Ion square

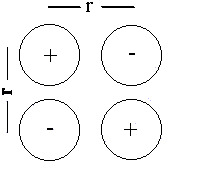
E_square = 4q₊q_–/4πε_or + q₊q₊/4πε_o√2r + q_–q_–/4πε_o√2r

Since (in this example) q₊=–q_–

E_square = q₊q_–(4 – 1/√2 – 1/√2)/4πε_or = 2.586E_dip

ion cube

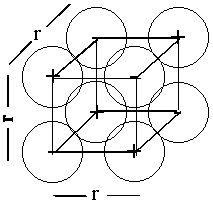
E_cube = 12q₊q_–/4πε_or + 6q₊q₊/4πε_o√2r + 6q_–q_–/4πε_o√2r + 4q₊q_–/4πε_o√3r

E_cube = q₊q_–(12 – 6/√2 – 6/√2 + 4/√3)/4πε_or = 5.824E_dip

Continue this over the entire lattice to give:

E_Coul = N₀MZ⁺Z^–e²/4πε_or

N₀ = Avogadro's number

Z⁺, Z^- are the ionic charges in units of e (i.e., +1, +2, -1, -2, etc.)

r is the interionic distance

M is called the Madelung constant.

M depends solely on geometry, i.e., the kind of lattice but the internuclear distances are factored out. Madelung constants are tabulated for all the common lattice types.

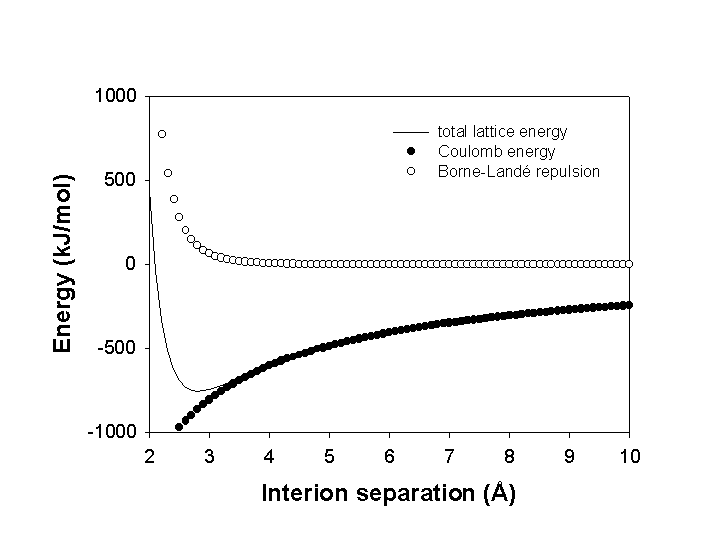
E_Coul is negative (all terms are positive except Z^–), i.e., the bonding is favorable. In fact, too favorable: the most stable situation is when r = 0.

Why? Initial point charge assumption does not allow for nuclear-nuclear repulsion at close distances.

Correct this empirically: add a term that is repulsive at small r but negligible at larger distances. This means either an exponential term or a 1/rⁿ term with large n.

Born repulsion:

E_rep = B/rⁿ

n is known as the Born exponent, B is an arbitrary constant

The lattice energy becomes

E_lat = E_Coul + E_rep = N₀MZ⁺Z^–e²/4πε_or + B/rⁿ

Need to find two new quantities: B and n.

Evaluate B at equilbrium because ∂E_lat/∂r = 0 at r = r_o (r_o is the equilibrium internuclear distance measured experimentally)

∂E_lat/∂r = –N₀MZ⁺Z^–e²/4πε_or² – nB/rⁿ⁺¹ = 0 at r = r_o

Thus, nB/r_oⁿ⁺¹ = –N₀MZ⁺Z^–e²/4πε_or_o²

B = –N₀MZ⁺Z^–e²r_oⁿ⁺¹/4πε_onr_o² = –N₀MZ⁺Z^–e²r_o^n–1/4πε_on

So, at r = r_o

E_lat = N₀MZ⁺Z^–e²/4πε_or + B/rⁿ = N₀MZ⁺Z^–e²/4πε_or_o + (–N₀MZ⁺Z^–e²r_o^n–1/4πε_on)/r_oⁿ

E_lat = N₀MZ⁺Z^–e²/4πε_or_o – N₀MZ⁺Z^–e²/4πε_onr_o

E_lat = N₀MZ⁺Z^–e²(1 – 1/n)/4πε_or_o

To find n, we must move away from the equilibrium position. The slope of the energy/distance curve on the low r side is primarily determined by n in the repulsion term. Experimentally, this can be obtained by compressing the sample, i.e. measuring the compressibility, κ:

κ = –(1/V_o)(∂V/∂P)_T (V_o = equilibrium molar volume; V = volume, P = pressure, T = temperature)

It can be shown that κ = (4πε_o)(18r_o⁴)/Me²(n – 1)

Compressibilities in ionic compounds are quite small:

Another common approach term is using the Born-Mayer repulsion: E_rep = Ae^–d*/r

Using the same approach as above this gives: E_lat = N₀MZ⁺Z^–e²(1 – d*/r_o)/4πε_or_o

d* is typically assigned a value of 34.5 pm

Sample calculation for NaCl:

4πε_o = 1.113×10^–10 J^–1C²m^–1

e = 1.602×10^–19 C

M = 1.74756 (NaCl structure)

d = 5.628×10^–10 m giving r_o = 2.814×10^–10 m

κ = 4.18×10^–11 N^–1m²

n is found by

n = 1 + (4πε_o)(18r_o⁴)/Me²κ = 1 + (1.113×10^–10 J^–1C²m^–1)(18×(2.814×10^–10 m)⁴/ (1.74756)(1.602×10^–19 C)²(4.18×10^–11 N^–1m²)

n = 1 + 6.70 J^–1m³/N^–1m² = 1 + 6.70 N·m/J = 7.70 (N·m = J)

E_lat = N₀MZ⁺Z^–e²(1 – 1/n)/4πε_or_o = (6.022×10²³ mol^–1)(1.74756)(+1)(–1)(1.602×10^–19 C)²(1 – 1/7.70)/ (1.113×10^–10 J^–1C²m^–1)(2.814×10^–10 m)

E_lat = –750348 J/mol = –750.3 kJ/mol

This compares to 769.4 kJ/mole experimental (2.5% error)

lattice energies are thermodynamically negative but reported as positive values so this is typically reported as 750.3 kJ/mol

Using the Born-Mayer equation gives E_lat = 756.6 kJ/mol

Kapustinskii deduced that the Madelung constants were approximately correlated with the number of ions in the repeat unit. This led him to propose a lattice energy formula that does not need knowledge of the crystal structure:

E_lat = –1202νZ⁺Z^–[1 – 0.345/(r₊ + r_–)]/ (r₊ + r_–) where ν is the total number of ions in the repeat unit of the ionic compound and r₊ and r_– are the cationic and anionic radii, respectively, in units of Å giving E_lat in units of kJ/mol

Note that r₊ + r_– = r_o

For NaCl, ν = 2 and r₊ + r_– = 2.814 Å

E_lat = –1202(2)(+1)(–1)[1 – 0.345/2.814]/2.814 = 741.6 kJ/mol