Answer

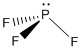
a. PF₃

Point Group: C_3v

C3v	E	2C3	3σv
a1	1	1	1	z	x2 + y2, z2
a2	1	1	–1	Rz
e	2	–1	0	(Rx, Ry) (x, y)	(x2–y2, xy) (xz,yz)
σ bonds	3	0	1

n(a₁) = [(1)(1)(3) + (2)(1)(0) + (3)(1)(1)]/6 = 1

n(a₂) = [(1)(1)(3) + (2)(1)(0) + (3)(–1)(1)]/6 = 0

n(e) = [(1)(2)(3) + (2)(–1)(0) + (3)(0)(1)]/6 = 1

Thus, the σ orbitals transform as a₁ + e

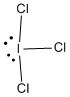
b. ICl₃

Point Group: C_2v

C2v	E	C2	σv (xz)	σv' (yz)
a1	1	1	1	1	z	x2, y2, z2
a2	1	1	–1	–1	Rz	xy
b1	1	–1	1	–1	Ry x	xz
b2	1	–1	–1	1	Rx y	yz
σ bonds	3	1	3	1

n(a₁) = [(1)(1)(3) + (1)(1)(1) + (1)(3)(1) + (1)(1)(1)]/4 = 2

n(a₂) = [(1)(1)(3) + (1)(1)(1) + (1)(–1)(3) + (1)(–1)(1)]/4 = 0

n(b₁) = [(1)(1)(3) + (1)(–1)(1) + (1)(1)(3) + (1)(–1)(1)]/4 = 1

n(b₂) = [(1)(1)(3) + (1)(–1)(1) + (1)(–1)(3) + (1)(1)(1)]/4 = 0

Thus, the σ orbitals transform as 2a₁ + b₁