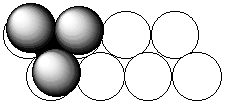Chemistry 401
Intermediate Inorganic Chemistry
University of Rhode Island
Practice Problems
Solids, Ionic Bonding
1. Which of the following schemes for the repeating pattern of close-packed planes are not ways of generating close-packed lattices? (a) ABCABC ...; (b) ABAC ...; (c) ABBA ...; (d) ABCBC ...; (e) ABABC...; (f) ABCCB ... .
(a) ABCABC ... is close-packed - this is the ccp lattice.
(b) ABAC ... is close-packed - the fourth layer (C) is just the other alternative for the placement of the B layer.
(c) ABBA ... is not close-packed - the adjacent B layers are not sphere to crevice.
(d) ABCBC ... is close-packed - this is similar to case (b).
(e) ABABC ... is close-packed - this is the same as (d).
(f) ABCCB ... is not close-packed - the adjacent C layers are not sphere to crevice.
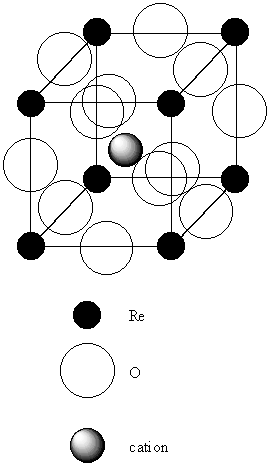
2. In the structure of MoS2, the S atoms are arranged in close-paced layers that repeat themselves in the sequence AAA... . The Mo Atoms occupy holes with C.N. = 6. Show that each Mo atom is surrounded by a trigonal prism of S atoms.
A schematic of the structure is shown below:
The open circles represent the first layer of S atoms, the shaded circles the second layer of S atoms, and the filled circle a Mo atom. Above and below each Mo atom is a triangle of S atoms, accounting for C.N. = 6. The arrangement of triangles of S on top of each other is the trigonal prism. (If the triangular layers were rotated by 60° relative to each other, then the coordination sphere about the Mo would be octahedral.)
3. The Coulombic attraction of nearest-neighbor cations and anions accounts for the bulk of the lattice enthalpy of an ionic compound. With this fact in mind, estimate the order of increasing lattice enthalpy of (a) MgO, (b) NaCl, (c) AlN, all of which crystallize in the rock-salt structure. Give your reasoning.
The nearest neighbor Coulombic attraction depends upon the ion charges and the distance between the ions. The changes in distance between ions is relatively small compared to the unit changes found in the ion charges, so MgO (+2, –2) has a roughly 4× larger lattice enthalpy than NaCl and AlN (+3, –3) has roughly 9× the lattice enthalpy of NaCl. Thus, the predicted order of lattice enthalpies is: NaCl < MgO < AlN.
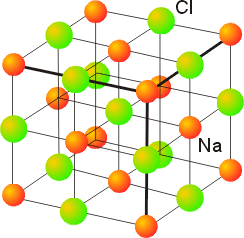
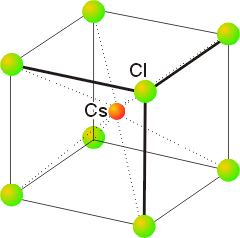
4. Depending upon the temperature, RbCl can exist in either the rock-salt or cesium-chloride structure. (a) What is the coordination number of the anion and cation in each of these structures? (b) In which of these structures will Rb have the higher apparent radius?
The rock-salt structure is closest-packed, as shown below:
The cations occupy the octahedral holes, so have 6 nearest neighbor anions and a coordination number of 6. In the unit cell shown above, the atom labeled Na, which would be Rb for RbCl, has 5 of the 6 nearest neighbors shown. The anions also have 6 nearest neighbors that are cations, so also have a coordination number of 6. The atom labeled Cl has 4 of the 6 nearest neighbors shown.
The cesium-chloride structure, as shown below, is not closest packed:
The cation at the center of the unit cell has 8 nearest neighbors (all shown), so the coordination number is 8. The chlorides also have 8 nearest neighbors, the cations in the center of all the surrounding unit cells.
Rb will have the larger radius in the CsCl structure because of the larger steric repulsion associated with C.N. = 8.
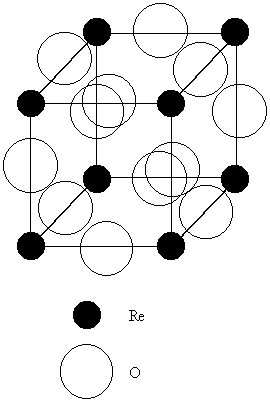
5. The ReO3 structure is cubic with Re at each corner of the unit cell and one O atom on each unit cell edge midway between the Re atoms. Sketch this unit cell and determine (a) the coordination number of the cation and anion and (b) the identity of the structure type that would be generated if a cation were inserted in the center of the ReO3 structure.
(a) A sketch of the ReO3 structure, as described, is shown below:
Each Re6+ ion has six nearest neigbor oxygen atoms, so the coordination number = 6.
Each O2– ion has two nearest neighbor rhenium atoms, so the coordination number = 2.
(b) A sketch of the structure with an additional cation added to the center of the unit cell is shown below:
This is exactly the same structure as the perovskite structure.
6. Given the following data for the length of a side of the unit cell for compounds that crystallize in the rock-salt structure, determine the cation radii: MgSe (545 pm), CaSe (591 pm), SrSe (623 pm), BaSe (662 pm). (Hint: To determine the Se2– radius, assume that the Se2– ions are in contact in MgSe.)
The rock-salt structure is given below:
In this case the Se2– ions take the place of chloride and the M2+ ions take the place of sodium ions. The unit cell length in all cases is found from two cation radii and two anion radii, i.e. length = 2r+ + 2r–. In the case of MgSe, the assumption is made that the anions are touching, so half the unit cell length gives the sides of an isosceles right triangle with hypotenuse equal to twice the anion radius, i.e. (length/2)2 + (length/2)2 = (2r–)2. Then, for the other salts the anion radius is assumed to be unchanged.
saltanion radius (pm)cation radius (pm)
MgSer– = √{¼[(545/2)2 + (545/2)2]} = 193 r+ = ½[545 – 2(193)] = 80
CaSe193 r+ = ½[591 – 2(193)] = 103
SrSe193 r+ = ½[623 – 2(193)] = 119
BaSe193 r+ = ½[662 – 2(193)] = 138
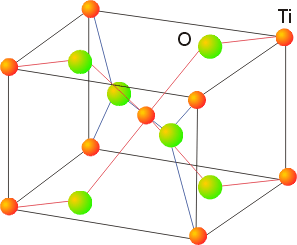
7. Confirm that in rutile (TiO2) the stoichiometry is consistent with the structure.
The rutile structure:
Inside each unit cell, there is 1 Ti in the center of the cell and 1/8 of a Ti at each corner, so there is a total of 1 + 8(1/8) = 2 Ti inside each unit cell. 2 of the O atoms are completely in the unit cell and 4 of the O atoms have ½ of the atom in the cell, giving 2 + 4(1/2) = 4 O atoms. Thus, each unit cell has a stoichiometry of Ti2O4, or 2 TiO2 per unit cell.
8. Estimate the lattice energy for magnesium chloride using both the Born-Landé equation and using a Born-Haber cycle. The heat of formation for magnesium chloride is –641.3 kJ/mole and the other thermodynamic data can be found in your textbook. In the Born-Landé equation, assume a fluorite structure, n= 8, and an interion distance of 2.4 Å. Compare the two values and comment about the agreement or disagreement.
The following reactions are required for the Born-Haber cycle: (the thermodynamic data can be found in the textbook)
Mg(s) + Cl2(g) → MgCl2(s) ΔHfo = –641.3 kJ/mol
Mg(s) → Mg(g) S = 148 kJ/mol
Mg(g) → Mg2+(g) IP1 + IP2 = 2187 kJ/mol
Cl2(g) → 2 Cl(g) D = 244 kJ/mol
2 Cl(g) → 2 Cl–(g) –2EA = –2(355) = –710 kJ/mol
Mg2+(g) + 2 Cl–(g) → MgCl2(s) –Elattice
S + IP1 + IP2 + D – 2 EA –Elatttice – ΔHfo = 0
Elatttice = S + IP1 + IP2 + D – 2 EA – ΔHfo = 148 + 2187 + 244 – 710 – (–641.3) = 2510 kJ/mol
The values to be used in the Born-Landé equation are:
No = 6.022×1023
Z+ = +2
Z– = –1
e = 1.602×10–19
M = 2.519
εo = 8.854×10–12
d = 2.4×10–10
n = 8
Plugging these values into the Born-Landé equation gives:
Elattice = –(6.022×1023)(2)(–1)(1.602×10–19)2(2.519)/ (4)(3.14159)(8.854×10–12)(2.4×10–10)×[1 – 1/8]
= 2551 kJ/molThe agreement between the experiment and the theory is excellent, which is quite surprising since magnesium chloride does not possess the fluorite structure!.
9. Calculate the lattice energy (in units of kJ/mol) for ZnO in the wurtzite structure using the Born-Landé equation and using a Born-Haber cycle. Compare the two answers and comment on any differences. Useful data: the Born exponent, n, = 8; the sublimation energy of zinc = 130.4 kJ/mol; and the standard heat of formation of zinc(II) oxide = –350.5 kJ/mol. Other data can be found in the textbook.
For the theoretical calculation using the Born-Landé equation:
Elat = –[(N0Z+Z–e2A)/(4πε0d0)](1 – 1/n)
N0 = 6.022×1023
Z+ = +2
Z– = –2
e = 1.602×10–19
A = 1.641 for the wurtzite structure
4πε0 = 1.113×10–10
d0 = 75 + 124 = 199 pm (for coordination number = 4) = 1.99×10–10 m
n = 8
Elat = –[(6.022×1023)(2)(–2)(1.602×10–19)2(1.641)/ (1.113×10–10)(1.99×10–10)](1 – 1/8) = 4008000 J/mol = 4008 kJ/mol
Using the Born-Haber cycle:
Zn(s) + ½ O2(g) → ZnO(s) ΔH°f = –350.5 kJ/mol
Zn(s) → Zn(g) S = 130.4 kJ/mol
Zn(g) → Zn+(g) IE1 = (9.393 eV)(96.485 kJ/mol/eV) = 906.3 kJ/mol
Zn+(g) → Zn2+(g) IE2 = (17.96 eV)(96.485 kJ/mol/eV) = 1733 kJ/mol
½ O2(g) → O(g) ½D = ½(497) = 248.5 kJ/mol
O(g) → O–(g) EA1 = 141 kJ/mol
O–(g) → O2–(g) EA2 = –780 kJ/mol
Zn2+(g) + O2–(g) → ZnO(s) –Elat
S + IE1 + IE2 + ½D – EA1 – EA2 – Elat – ΔH°f = 0
Elat = 130.4 + 906.3 + 1733 + 248.5 – 141 – (–780) – (–350.5) = 4008 kJ/mol
The agreement between theory and experiment is remarkable!
10. LiI is found to have the same structure as NaCl. Given this information, estimate the lattice energy for LiI using the Born-Mayer equation and d* = 34.5 pm. Radius ratio rules suggest that the the observed LiI structure is anomalous; explain why.
The ionic radius for Li+ (CN = 6 for the NaCl structure) = 76 pm and the ionic radius for I– (CN = 6 for the NaCl structure) = 206 pm, so do = 76 + 206 = 282 pm = 2.82 × 10–10 m. For the rock salt (NaCl) stucture, A = 1.748. Z+ = +1 and Z– = –1. The physical constants are N0 = 6.022 × 1023, e = 1.602 × 10–19, 4πε0 = 1.113 × 10–10, and d* = 34.5 pm. Then:
–Elat = N0Ae2Z+Z–/4πε0do×(1 – d*/do)
Elat = –(6.022 × 1023)(1.748)(1.602 × 10–19)2(+1)(–1)/ (1.113 × 10–10)(2.82 × 10–10)×(1 – 34.5/282)
Elat = 755400 J/mole = 755.4 kJ/mole
The radius ratio for LiI is ρ = 76/206 = 0.37 suggesting that the Li+ should occupy the tetrahedral holes while it is observed that the cations occupy the octahedral holes. If the Li+ were to occupy the tetrahedral holes and adopt the ZnS structure, as suggested by the radius ratio rules, the calculated lattice energy would be ~747 kJ/mole. The rock salt structure is slightly favored thermodynamically.
11. In the context of band theory, explain why Mg is a metal, despite the fact that it has a filled s2 electron configuration.
The valence orbitals for Mg are 3s and 3p. When the atom condenses into the solid state all of the valence orbitals overlap to form bands and the bottom of the lowest energy p band is lower than the top of the s band. This allows electrons to occupy both the s band and one of the p bands, so that both bands are partially occupied. Since no band is filled, Mg has the properties of a metal.
12. Look up the metallic radius for the first row transition metal elements (Sc to Zn) and explain the trend in terms of metallic bonding.
The metallic radii are (from the textbook):
Metalrmet (pm)Electron Configuration Z*
Sc164[Ar]4s23d1 4.632
Ti147[Ar]4s23d2 4.817
V135[Ar]4s23d3 4.981
Cr129[Ar]4s13d5 5.133
Mn137[Ar]4s23d5 5.283
Fe126[Ar]4s23d6 5.434
Co125[Ar]4s23d7 5.576
Ni125[Ar]4s23d8 5.711
Cu128[Ar]4s13d10 5.858
Zn137[Ar]4s23d10 5.576
Two competing effects are occurring as the elements change from Sc to Zn. The atomic orbitals used to create the band structure are the 4s and 3d (and perhaps the 4p, as well) so there are at least six overlapping bands. As the electrons fill these bands, initially more bonding states are occupied so the metallic radius decreases since there is more bonding character to attract atoms together. Near the middle of the series nonbonding states are occupied, so there should be little change in the metallic radius. Finally, at the end of the transition series the electrons are being used to fill antibonding states so the bonding between atoms decreases and the radius increases. Competing with this is the effect of Z*. As the atomic number increases Z* increases, nearly linearly, across the entire series. This causes a reduction in orbital size, which decreases the atomic radius and will reduce the amount of overlap between neighboring orbitals. Thus, the observed trend mainly follows the prediction based on band arguments from Sc to Fe but the constancy of the radius through Cu is caused by the approximate cancelation of the antibonding effects with the Z* effects.
13. Gallium arsenide is a semiconductor that is widely used for the construction of the red-light-emitting displays and is under development for advanced central processor chips in supercomputers. If gallium arsenide (GaAs) is doped with selenium (on the As site), is it n-doped or p-doped?
Se has more valence electrons than As (or Ga, for that matter) so introduces extra electrons into the lattice, thereby making it an n-doped system.
14. The promotion of an electron from the valence band into the conduction band in pure titanium(IV) oxide by light absorption requires a wavelength of less than 350 nm. Calculate the energy gap in electronvolts between the valence and conduction bands.
The band gap corresponds to the energy of the absorbed wavelength of light, or E = hc/λ
h = 6.626×10–34 J s
c = 2.9929×108 m/s
λ = 350 nm = 3.50×10–7 m
so E = (6.626×10–34)(2.9929×108)/(3.50×10–7) = 5.68×10–19 J/molecule
In units of eV, 1 eV = 1.602×10–19 J/molecule so E = 5.68×10–19 J/molecule/1.602×10–19 J/molecule/eV = 3.54 eV
15. When titanium(IV) oxide is heated in hydrogen, a blue color develops, indicating light absorption in the red. Does reduction of Ti(IV) to Ti(III) correspond to n-doping or p-doping?
Reduction causes a apparent decrease in the band gap, as evidenced by the absorption of the low energy red light (compared to the original titanium(IV) oxide, which absorbs light in the UV at 350 nm. Reduction also introduces extra electrons into the lattice, formally in the form of Ti(III). An excess of electrons is the signature of an n-type semiconductor.