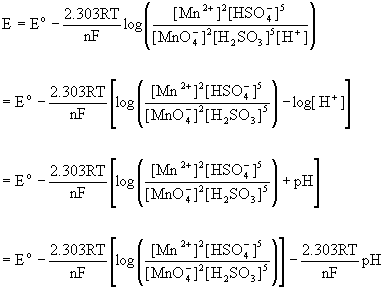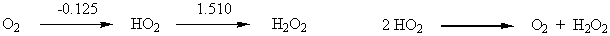1. Some anaerobic bacteria utilize oxidizing agents other than O2 as an energy source; for example, SO42–, NO3–, and Fe3+. One half-reaction is FeO(OH)(s) + HCO3–(aq) + 2 H+(aq) + e– → FeCO3(s) + 2 H2O(l), for which E° = +1.67 V. What mass of iron gives the same standard reaction Gibbs energy as 1.00 g of oxygen?
The standard half-reaction for the reduction of oxygen under acid conditions is:
O2(g) + 4 H+(aq) + 4 e– → 2 H2O(l)
for which E° = +1.23 V. 1.00 g of oxygen = 0.03125 moles, which would give 0.125 moles of electrons. Thus, the Gibbs energy is:
ΔG° = –nFE° = –(0.125)(96485)(1.23) = 14.8 kJ
To obtain the same free energy from the iron reaction would require n = ΔG°/FE° = (14800)/(96485)(1.67) = 0.0919 moles of electrons. Since the mole ratio between iron and electrons is 1, this is also the number of moles of iron required, or 5.13 g.
2. Using the following aqueous acid solution reduction potentials E° (Pd2+, Pd) = +0.915 V and E° ([PdCl4]2–, Pd) = +0.600 V, calculate the equilibrium constant for Pd2+(aq) + 4 Cl–(aq) →← [PdCl4]2–(aq) in 1 M HCl(aq).
Break the desired reaction into two components that use the available potential information:
Pd2+(aq) + 2 e– → Pd(s) E° = +0.915 V
Pd(s) + 4 Cl–(aq) → [PdCl4]2–(aq) + 2 e– E° = +0.600 V
Summing the two half-reactions gives the target reaction:
Pd2+(aq) + 4 Cl–(aq) →← [PdCl4]2–(aq)
and the 'potential' for the desired reaction is given by E° = +0.915 – 0.600 = +0.315 V. The equilibrium constant is found from the relationship E° = (RT/nF)lnK. Solving gives:
K = exp[nFE°/RT] = exp[(2)(96500)(0.315)/(8.314)(298)] = 4.5×1010
3. Many of the tabulated data for standard potentials have been determined from thermochemical data rather than direct electrochemical measurements of cell potentials. Carry out a calculation to illustrate this approach for the half-reaction Sc2O3(s) + 3 H2O(l) + 6 e– → 2 Sc(s) + 6 OH–(aq).
Sc3+(aq) OH–(aq) H2O(l) Sc2O3(s) Sc(s)
ΔHf° (kJ/mol)–614.2 –230.0 –285.8 –1908.7 0
Sm°(J K–1mol–1)–255.2 –10.75 +69.91 +77.0 +34.76
Direct calculation of the reduction potential from the half-cell is not possible because the heat of formation and absolute entropy for the electron are not known. Thus, an oxidation reaction with known potential must be used:
Sc(s) → Sc3+(aq) + 3e– E° = 2.03 V
Multiplying by 2 and adding this to the unknown reaction gives a net reaction of
Sc2O3(s) + 3 H2O(l) → 2 Sc3+(aq) + 6 OH–(aq)
The heat of reaction for the net reaction is:
ΔH° = [2ΔfH°(Sc3+(aq)) + 6ΔfH°(OH–(aq))] – [ΔfH°(Sc2O3(s)) + 3ΔfH°(H2O(l))]
= [2(–614.2) + 6(–230.0)] – [(–1908.7) + 3(–285.8)] = +157.7 kJ mol–1
The change in entropy for the net reaction is:
ΔS° = [2 Sm°(Sc3+(aq)) + 6 Sm°(OH–(aq))] – [Sm°(Sc2O3(s)) + 3 Sm°(H2O(l))]
= [2(–255.2) + 6(–10.75)] – [(+77.0) + 3(+69.91)] = –861.6 J K–1 mol–1
At 298 K:
ΔG° = ΔH° – TΔS° = +157.7 – (298)(–0.8616) = +414.5 kJ mol–1
ΔG° = ΔG°reduction + ΔG°oxidation = ΔG°reduction + –nFE°
414500 J mol–1 = ΔG°reduction – (6)(96485)(2.03)
ΔG°reduction = 414500 + 1175000 = 1590000 J mol–1
E°reduction = –1590000/(6)(96485) = –2.75 V
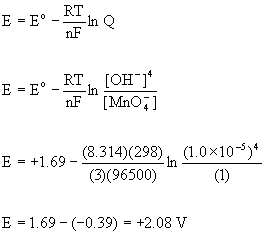
4. Calculate the reduction potential at 25 °C for the conversion of MnO4–(aq) to MnO2(s) in aqueous solution at pH = 9.00 and 1 M MnO4–(aq) given that E°(MnO4–, MnO2) = +1.69 V.
The balanced half-reaction under basic conditions is:
MnO4–(aq) + 2 H2O(l) + 3 e– → MnO2(s) + 4 OH–(aq)
To find the potential at pH = 9.00 ([OH–] = 1.0×10–5 M) the Nernst equation must be used.
5. Balance the following redox reaction in acid solution: MnO4–(aq) + H2SO3(aq) → Mn2+(aq) + HSO4–(aq). Predict the qualitative pH dependence on the net potential for this reaction (i.e. increases, decreases, remains the same).
Split the reaction into the two half-reactions and balance each separately:
MnO4–(aq) + 8 H+(aq) + 5 e– → Mn2+(aq) + 4 H2O(l)
H2SO3(aq) + H2O(l) → HSO4–(aq) + 3 H+(aq) + 2 e–
so the net reaction is:
2 MnO4–(aq) + 5 H2SO3(aq) + H+(aq) → 2 Mn2+(aq) + 5 HSO4–(aq) + 3 H2O(l)
Since hydrogen ion is a reactant, an increase in pH lowers the hydrogen ion concentration, driving the reaction towards reactants, thereby decreasing the net potential.
This can be thought of in terms of the Nernst equation, as well:
That is, increasing the pH subtracts from the standard potential so the net potential decreases with increasing pH.
6. From the following Latimer diagram, calculate the net E° value for the reaction 2 HO2(aq) → O2(g) + H2O2(aq)
Given your value of E°, comment on the thermodynamic tendency of HO2 to undergo disproportionation.
For the disproportionation reaction E° = +0.125 + 1.510 = + 1.635 V. This is a large positive value so the disproportionation is strongly favored thermodynamically.
7. Comment on the likelihood that the following reactions occur by a simple out-sphere electron transfer, simple atom transfer, or a multistep mechanism:
(a) HIO(aq) + I–(aq) → I2(aq) + OH–(aq)
(b) [Co(phen)3]3+(aq) + [Cr(bipy)3]2+(aq) → [Co(phen)3]2+(aq) + [Cr(bipy)3]3+(aq)
(c) IO3–(aq) + 8 I–(aq) + 6 H+(aq) → 3 I3–(aq) + 3 H2O(l)
(a) HIO(aq) + I–(aq) → I2(aq) + OH–(aq)
This reaction is probably a simple atom transfer. The iodine atom in HIO bonds to the iodide ion to form the iodine molecule, leaving hydroxide ion behind.
(b) [Co(phen)3]3+(aq) + [Cr(bipy)3]2+(aq) → [Co(phen)3]2+(aq) + [Cr(bipy)3]3+(aq)
This reaction is almost certainly a simple outer-sphere electron transfer. Both reactants have relatively small metal ions from the first transition series bound with bulky Lewis bases, which prevents any inner-sphere bond formation for steric reasons. Further, the phen and bipy Lewis bases do not have any available lone pairs to bond to a neighboring reactant to form an inner-sphere transition state.
(c) IO3–(aq) + 8 I–(aq) + 6 H+(aq) → 3 I3–(aq) + 3 H2O(l)
This is a multistep mechanism. Given the stoichiometry, it is unlikely that a single electron transfer step, either outer-sphere or inner-sphere, could transfer the required atoms and electrons from one transition state.
8. Complete and balance the following oxidation-reduction reactions.
a) H2O2(aq) → O2(g) (pH = 0)
b) MnO4–(aq) + C2O42–(aq) → CO2(g) + Mn2+(aq) (pH = 0)
c) MnO4–(aq) + CH3CH2OH(aq) → CH3CHO(aq) + MnO2(s) (pH = 14)
a) H2O2(aq) → O2(g) (pH = 0)
Reduction half-reaction: H2O2(aq) + 2 H+(aq) + 2 e– → 2 H2O(l)
Oxidation half-reaction: H2O2(aq) → O2(g) + 2 H+(aq) + 2 e–
Net reaction: 2 H2O2(aq → O2(g) + 2 H2O(l)
b) MnO4–(aq) + C2O42–(aq) → CO2(g) + Mn2+(aq) (pH = 0)
Reduction half-reaction: MnO4–(aq) + 8 H+(aq) + 5 e– → Mn2+(aq) + 4 H2O(l)
Oxidation half-reaction: C2O42–(aq) → 2 CO2(g) + 2 e–
Net reaction: 2 MnO4–(aq) + 5 C2O42–(aq) + 16 H+(aq) → 2 Mn2+(aq) + 10 CO2(g) + 8 H2O(l)
c) MnO4–(aq) + CH3CH2OH(aq) → CH3CHO(aq) + MnO2(s) (pH = 14)
Reduction half-reaction: MnO4–(aq) + 4 H+(aq) + 3 e– → MnO2(s) + 2 H2O(l)
Oxidation half-reaction: CH3CH2OH(aq) → CH3CHO(aq) + 2 H+(aq) + 2 e–
Net reaction (in acid): 2 MnO4–(aq) + 3 CH3CH2OH(aq) + 2 H+(aq) → 2 MnO2(s) + 3 CH3CHO(aq) + 4 H2O(l)
Acid/base neutralization: 2 H2O(l) → 2 H+(aq) + 2 OH–(aq)
Net reaction (in base): 2 MnO4–(aq) + 3 CH3CH2OH(aq) → 2 MnO2(s) + 3 CH3CHO(aq) + 2 H2O(l) + 2 OH–(aq)
