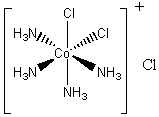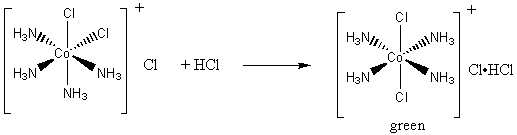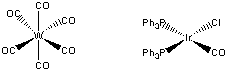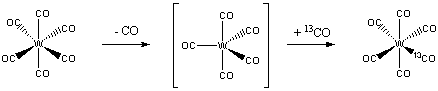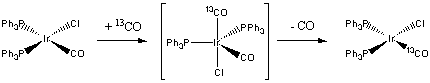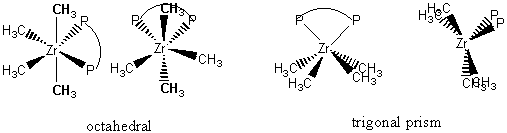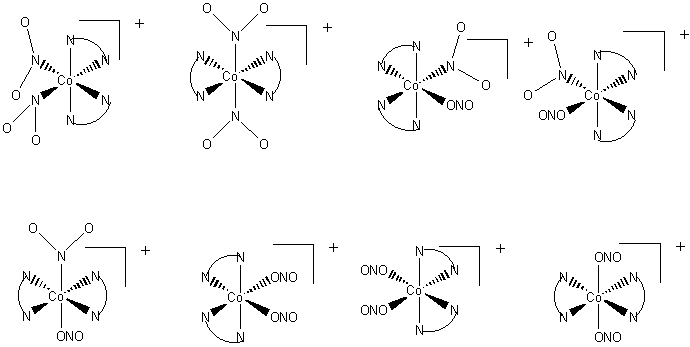Chemistry 401
Intermediate Inorganic Chemistry
University of Rhode Island
Practice Problems
d-Metal Complexes
1. (a) Sketch the two structures that describe most six-coordinate complexes. (b) Which one of these is rare?
(a) The two structure types for six-cordinate complexes are octahedral and trigonal prismatic, shown below:
(b) The trigonal prism is the rare structure
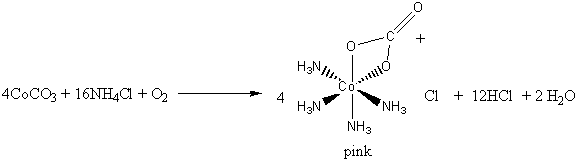
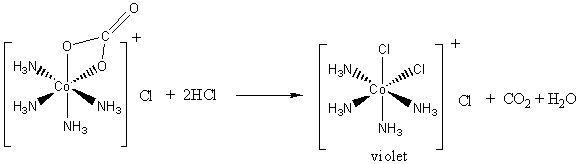
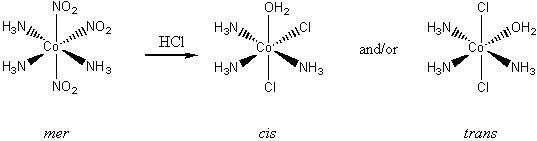
2. Air oxidation of Co(II) carbonate and aqueous ammonium chloride gives a pink chloride salt with a ratio of 4 NH3 : Co. On addition of HCl to a solution of this salt, a gas is rapidly evolved and the solution slowly turns violet on heating. Complete evaporation of the violet solution yields CoCl3·4NH3. When this compound is heated in concentrated HCl, a green salt can be isolated with composition CoCl3·4NH3·HCl. Write balanced equations for all transformations occurring after the air oxidation. Give as much information as possible about the isomerism occurring and the basis for your reasoning. Is it helpful to know that the form of [Co(en)2Cl2]+ that is resolvable into enantiomers is violet?
The hint concerning the color of [Co(en)2Cl2]+ is useful because the enantiomerically resolvable form of this ion must be the cis isomer (the trans isomer is not optically active). This suggests that the violet salt, CoCl3·4NH3, must have a cis structure, as well, shown below.
The air oxidation of CoCO3 gives the pink cis-chelate complex:
Addition of HCl causes an acid/base reaction with the carbonate ligand, releasing carbon dioxide and maintaining the cis geometry (the violet complex alluded to by the hint):
The final green product is the correct color for a trans complex, so the concentrated HCl must be inducing a cis-trans isomerization:
3. The equilibrium constants for the successive reactions of ethylenediamine with Co2+, Ni2+, and Cu2+ are as follows.
[M(OH2)6]2+(aq) + en(aq) →← [M(en)(OH2)4]2+(aq) + 2 H2O(l) K1
[M(en)(OH2)4]2+(aq) + en(aq) →← [M(en)2(OH2)2]2+(aq) + 2 H2O(l) K2
[M(en)2(OH2)2]2+(aq) + en(aq) →← [M(en)3]2+(aq) + 2 H2O(l) K3
Ionlog K1 log K2log K3
Co2+5.89 4.833.10
Ni2+7.52 6.284.26
Cu2+10.72 9.31–1.0
Discuss whether the data support the generalizations in the text about successive formation constants and the Irving-Williams series.
How do you account for the very low value of K3 for Cu
As the number of en ligands increases the step-wise formation constant decreases for each ion, as expected based on entropy considerations (and perhaps somewhat on steric grounds). As the atomic number of the metal increases the step-wise formation increases for K1 and K2, which is primarily a Z* effect and in complete agreement with the Irving-Williams series. K3 for Cu2+ is out of line because Cu2+ does not easily form six-coordinate complexes because of the extreme Jahn-Teller distortion found in these complexes.
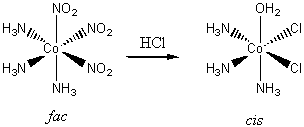
4. When cobalt(II) salts are oxidized by air in a solution containing ammonia and sodium nitrite, a yellow solid, [Co(NO2)3(NH3)3], can be isolated. In solution it is nonconducting; treatment with HCl gives a complex that, after a series of further reactions, can be identified as trans-[CoCl2(NH3)3(OH2)]+. It requires an entirely different route to prepare cis-[CoCl2(NH3)3(OH2)]+. Is the yellow substance fac or mer? What assumption must you make to arrive at a conclusion?
Consider the two possibilities for the yellow complex. If the complex is mer, then the possible products are either cis or trans:
If the yellow complex is fac, then only a cis product is possible:
Since a trans product was found, the original yellow complex must have been mer since this is the only one that allows a trans product.
The assumption in this line of reasoning is that the substitutions on the cobalt by water and chloride are at the same positions as the nitrite, i.e., there is no scrambling of the ligands during the reaction processes.
5. Decide which of the two complexes (a) W(CO)6 or (b) IrCl(PPh3)2(CO) should undergo the fastest exchange with 13CO. Justify your answer.
First, draw the structures of each complex:
W(CO)6 is an 18 electron complex, so will be rather unreactive to either associative or dissociative routes. Since the complex is six-coordinate, the likely reaction mechanism will be via a dissociative route:
IrCl(PPh3)2(CO) is a four-coordinate, 16 electron complex. Addition of a 13CO forms an 18 electron intermediate, which should be relatively favorable:
Thus, the iridium complex is predicted to exchange CO much more rapidly than the tungsten complex.
6. The reaction of [ZrCl4(dppe)] (dppe is a bidentate phosphine ligand) with Mg(CH3)2 gives [Zr(CH3)4(dppe)]. NMR spectra indicate that all the methyl groups are equivalent. Draw octahedral and trigonal prism structures for the complex and show how the conclusion from NMR supports the trigonal prism structure. (P. M. Morse and G. S. Girolami, J.Am. Chem. Soc., 1989, 111, 4114.)
Two different perspectives of each structure is shown. In the octahedral structure there are 2 different sets methyl groups (bold and not bold) that are inequivalent, i.e., there is no symmetry operation that relates the two sets of methyl groups (within each set, a C2 axis exchanges the each pair, so each pair is equivalent). In the trigonal prism structure all four methyl groups are equivalent: front and back are related by mirrors, right and left are related by mirrors, and across the front-back diagonal there is a C2 axis.
7. For each of the following pairs of complexes, indicate the one that has the larger LFSE:
(a) [Cr(OH2)6]2+ or [Mn(OH2)6]2+
(b) [Mn(OH2)6]2+ or [Fe(OH2)6]3+
(c) [Fe(OH2)6]3+ or [Fe(CN)6]3–
(d) [Fe(CN)6]3– or [Ru(CN)6]3–
(e) tetrahedral [FeCl4]2– or tetrahedral [CoCl4]2–
Use the electron configuration and/or spectrochemical series to answer the questions asked.
(a) [Cr(OH2)6]2+ or [Mn(OH2)6]2+
Both complexes have the same ligands, water, which is a weak ligand, so the LFSE is determined by the electron configuration. Cr2+ is d4, or t2g3eg1 with LFSE = –6Dq while Mn2+ is d5, or t2g3eg2 with LFSE = 0. [Cr(OH2)6]2+ has the larger LFSE (more stabilization).
(b) [Mn(OH2)6]2+ or [Fe(OH2)6]3+
Both complexes have the same ligands, water, which is a weak ligand, and both are d5 or t2g3eg2 so the LFSE = 0 for both complexes.
(c) [Fe(OH2)6]3+ or [Fe(CN)6]3–
Both complexes have the same metal in the same oxidation state, Fe3+, which is d5. Water is a weak field ligand (high spin) so the electron configuration is t2g3eg2 with LFSE = 0. Cyanide is a strong field ligand (low spin) so the electron configuration is t2g5 with LFSE = –20Dq + 2P. [Fe(CN)6]3– has the larger LFSE (more stabilization).
(d) [Fe(CN)6]3– or [Ru(CN)6]3–
Both complexes have the same ligands, CN–, which is a strong field (low spin) ligand and the electron configurations for both metals are d5 so the LFSE = –20Dq + 2P. Ru3+ is higher on the Irving-Williams series (larger Z*) for metals than Fe3+ so the ruthenium complex will have the larger LFSE.
(e) tetrahedral [FeCl4]2– or tetrahedral [CoCl4]2–
Both complexes have the same ligands, chloride, which is a weak ligand (although this usually does not matter in a tetrahedral environment), so the LFSE is determined by the electron configuration. Fe2+ is d6, or e3t23 with LFSE = –6Dqt while Co2+ is d7, or e4t23 with LFSE = –12Dqt. Tetrahedral [CoCl4]2– has the larger LFSE (more stabilization).
8. (a) On a chart of the d-block elements in their periodic table arrangement, identify the elements and associated oxidation numbers that form square-planar complexes. (b) Give formulas for three examples of square-planar complexes.
(a) d-block portion of the Periodic Table with the ions that form square-planar complexes highlighted in yellow:
Sc Ti V Cr Mn Fe Co Ni
Ni2+Cu
Cu2+Zn Y Zr Nb Mo Tc Ru Rh
Rh+Pd
Pd2+Ag
Ag3+Cd La Hf Ta W Re Os Ir
Ir+Pt
Pt2+Au
Au3+Hg (b) Examples of square-planar complexes:
PtCl42–, Pt(NH3)42+, Ni(CN)42–, AuCl4–, Cu(NH3)42+, PdCl42–
9. Sketch all the possible isomers of [Co(en)2(NO2)2], including optical isomers, in which the en ligands are bidentate. Do not draw different orientations of the same isomer.
There are optical isomers when the nitrito groups are cis, geometric isomers when the nitrito groups are trans, and the nitrito groups are ambidentate, able to bond either through the N atom or an O atom.
10. Give the name and find the ligand field stabilization energy (in terms of Dq) for the following complexes:
a) [Cr(NH3)6]3+
b) [Cu(NH3)4(OH2)2]2+
c) [Ti(OH2)6]3+
d) [Co(CN)6]3– (low spin)
e) [Ni(NH3)4Cl2]
a) [Cr(NH3)6]3+
Hexaamminechromium(III) ion
The oxidation state of Cr is 3+ so the electron configuration is d3 (t2g3) so LFSE = –12Dq
b) [Cu(NH3)4(OH2)2]2+
trans–Tetraamminediaquacopper(II) ion or cis–tetraamminediaquacopper(II) ion
The oxidation state of Cu is 2+ so the electron configuration is d9 (t2g6eg3) so LFSE = –6Dq
c) [Ti(OH2)6]3+
Hexaaquatitanium(III) ion
The oxidation state of Ti is 3+ so the electron configuration is d1 (t2g1) so LFSE = –4Dq
d) [Co(CN)6]3– (low spin)
Hexacyanocobaltate(III) ion
The oxidation state of Co is 3+ so the electron configuration is d6 (t2g6) so LFSE = –24Dq + 2P
e) [Ni(NH3)4Cl2]
cis–Tetraamminedichloronickel(II) or trans–tetraamminedichloronickel(II)
The oxidation state of Ni is 2+ so the electron configuration is d8 (t2g6eg2) so LFSE = –12Dq
11. Predict which of the following complexes is Jahn-Teller active:
a) [Cr(NH3)6]3+
b) [Cu(NH3)4(OH2)2]2+
c) [Ti(OH2)6]3+
d) [Co(CN)6]3–
e) [Ni(NH3)4Cl2]
a) [Cr(NH3)6]3+: Cr3+, d3, Not Jahn-Teller active.
b) [Cu(NH3)4(OH2)2]2+: Cu2+, d9, Jahn-Teller active, probably will axially elongate.
c) [Ti(OH2)6]3+: Ti3+, d1, Jahn-Teller active, will axially compress.
d) [Co(CN)6]3–: Co3+, d6, low spin (cyanide is a strong ligand), Not Jahn-Teller active
e) [Ni(NH3)4Cl2]: Ni2+, d8, Not Jahn-Teller active
12. Predict which of the following complexes will be stable:
a) [Mo(CO)6]
b) [(η6–C6H6)2Cr]
c) [(η3–C3H5)Co(CO)2]
d) [Fe(diphos)(CO)3] (diphos = Ph2PCH2CH2PPh2, Ph = C6H5)
a) [Mo(CO)6]
Metal/Ligande– countTotal
Mo0d66
CO2×612
Total e–18, stable
b) [(η6–C6H6)2Cr]
Metal/Ligande– countTotal
Cr0d66
η6–C6H62×612
Total e–18, stable
c) [(η3–C3H5)Co(CO)2]
Metal/Ligande– countTotal
Co+d88
CO2×24
η3–C3H54×14
Total e–16, likely stable
d) [Fe(diphos)(CO)3] (diphos = Ph2PCH2CH2PPh2, Ph = C6H5)
Metal/Ligande– countTotal
Fe0d88
CO2×36
diphos4×14
Total e–18, stable
13. Find the LFSE in terms of Dq and calculate the spin-only magnetic moment (in units of Bohr-magnetons) for the following complexes:
a) cis–diaqua–cis–dichloro–cis–difluorocobaltate(II) ion
b) trans–dicyanobis(ethylenediamine)iron(III) ion
c) trans–dichlorotetrakis(triphenylphosphine)nickel(II)
d) tris(bipyridine)ruthenium(II) ion
e) cis–dicyanobis(oxalato)manganate(II) ion
All of these complexes are six-coordinate so we can treat them as octahedral. The LFSE is determined by the electron configuration and the ligand field strength of the ligands. The number of unpaired spins, n, found from the electron configuration is used to find the spin-only moment μ = [n(n+2)]½ μB
a) cis–diaqua–cis–dichloro–cis–difluorocobaltate(II) ion
Co2+ is d7 and these are all weak field ligands. therefore:
The electron occupation is t2g5eg2 so the LFSE = 8Dq
The number of unpaired electrons is 3, so μ = [3(3+2)]½ = 3.87 μB
b) trans–dicyanobis(ethylenediamine)iron(III) ion
Fe3+ is d5 and these are all strong field ligands. Therefore:
The electron occupation is t2g5eg0 so the LFSE = 20Dq – 2P
The number of unpaired electrons is 1, so μ = [1(1+2)]½ = 1.73 μB
c) trans–dichlorotetrakis(triphenylphosphine)nickel(II)
Ni2+ is d8 so the field strength of the ligands does not matter. Therefore:
The electron occupation is t2g6eg2 so the LFSE = 12Dq
The number of unpaired electrons is 2, so μ = [2(2+2)]½ = 2.83 μB
d) tris(bipyridine)ruthenium(II) ion
Ru2+ is d6 and these are strong field ligands. Therefore:
The electron occupation is t2g6eg0 so the LFSE = 24Dq – 2P
The number of unpaired electrons is 0, so μ = [0(0+2)]½ = 0 μB
e) cis–dicyanobis(oxalato)manganate(II) ion
Mn2+ is d5 and cyanide is a strong field ligand while oxalate is near the border. This suggests that the net will give a low-spin complex. Therefore:
The electron occupation is t2g5eg0 so the LFSE = 20Dq – 2P
The number of unpaired electrons is 1, so μ = [1(1+2)]½ = 1.73 μB
14. Predict whether the following complexes will be stable:
a) hexacarbonylvanadium(0)
b) bis(η5–cyclopentadienyl)bis(η1–cyclopentadienyl)titanium(IV)
c) bis(η4–cyclooctadiene)nickel(0)
d) hexacyanoferrate(III)
e) bis(η6–benzene)chromium(0)
Use the EAN rule to determine the stability of each of these complexes.
a) hexacarbonylvanadium(0)
V(0) is d5 in this complex.
Each CO contributes 2 electrons: total = 6(2) = 12
Total electron count = 5 + 12 = 17, predicted to be unstable. (In fact, V(CO)6 is stable – there is a disproportionation into [V(CO)6+ ][V(CO)6– ], giving 16 and 18 electron complexes.)
b) bis(η5–cyclopentadienyl)bis(η1–cyclopentadienyl)titanium(IV)
Ti(IV) is d0 in this complex.
Each η5–cp contributes 6 electrons: total = 2(6) = 12
Each η1–cp contributes 2 electrons: total = 2(2) = 4
Total electron count = 12 + 4 = 16, predicted to be stable.
c) bis(η4–cyclooctadiene)nickel(0)
Ni(0) is d10 in this complex.
Each η4–COD contributes 4 electrons: total = 2(4) = 8
Total electron count = 10 + 8 = 18, predicted to be stable.
d) hexacyanoferrate(III)
Fe(III) is d5 in this complex.
Each CN– contributes 2 electrons: total = 6(2) = 12
Total electron count = 5 + 12 = 17, predicted to be unstable. (It is stable, however; the EAN rule fails in this case.)
e) bis(η6–benzene)chromium(0)
Cr(0) is d6 in this complex.
Each benzene contributes 6 electrons: total = 2(6) = 12
Total electron count = 6 + 12 = 18, predicted to be stable.
15. Removing the all of the water from hydrates of transition metal complexes is notoriously difficult. Typically, simply heating the complex is ineffective and reaction with something like thionyl chloride is required. For example, cobalt(II) chloride hexahydrate only loses four water molecules to become cobalt(II) chloride dihydrate when heated in an oven at 150 °C. Suggest an explanation for this observation.
Although the chemical formula might suggest that waters in transition metal compounds are hydrates, often some of the waters act as ligands that chemically bond, in some cases fairly strongly, to the metal ion. In the case of CoCl2·6H2O, heating transforms the compound into the tetrahedral complex [CoCl2(H2O)2]. The bond strength between the Co2+ and the O in H2O is strong enough that 150 °C is not enough energy to break the bond.
16. Find the LFSE (in terms of Dq and P) for: a) tris(oxalato)chromate(III) ion; b) hexacyanoferrate(II) ion; c) tetrachloro–η2–etheneplatinate(II) ion.
a) tris(oxalato)chromate(III) ion
[Cr(ox)3]3– has Cr in the +3 oxidation state, which is d3, and approximately an octahedral crystal field so LFSE = –12Dq.
b) hexacyanoferrate(II) ion
[Fe(CN)6]4– has Fe in the +2 oxidation state, which is d6, and a strong octahedral crystal field so LFSE = –24Dq + 2P.
c) tetrachloro–η2–etheneplatinate(II) ion
[Pt(CH2=CH2)Cl4]2– has Pt in the +2 oxidation state, which is d8, and approximately an octahedral crystal field so LFSE = –12Dq.
17. Predict the stability of the following species: a) bis(η5–cyclopentadienyl)cobalt(II); b) tetracarbonylnickel(0); c) tricarbonyl(η5–cyclopentadienyl)manganese(I).
a) bis(η5–cyclopentadienyl)cobalt(II)
Using the EAN rule, Co(cp)2:
Co2+ is d7: 7 e–
cp– contributes 6 e– × 2: 12 e–
Total: 19 e–, not stable.
b) tetracarbonylnickel(0)
Using the EAN rule, Ni(CO)4:
Ni0 is d10: 10 e–
CO contributes 2 e– × 4: 8 e–
Total: 18 e–, stable.
c) tricarbonyl(η5–cyclopentadienyl)manganese(I)
Using the EAN rule, Mn(cp)(CO)3:
Mn+ is d6: 6 e–
cp– contributes 6 e– × 1: 6 e–
CO contributes 2 e– × 3: 6 e–
Total: 18 e–, stable.
18. Chromium (III) complexes are nearly all six-coordinate with octahedral geometry. Suggest a reason for this observation.
Cr3+ is d3 so that the LFSE is –12Dq independent of the strength of the ligand, which is largely thermodyamically favorable. Any reduction in the number of ligands will reduce the LFSE (for example, in tetrahedral coordination the LFSE drops by more than 50%), which is not favorable. Z* for Cr3+ will not be too different from Z (Cr is on the leftward side of the Periodic Table), which implies that the ionic radius will be large enough that the presence of six ligands does not bring about too much steric repulsion. Yet, since Cr is a first row transition metal, the ionic radius is still small enough that the coordination sphere can not expand to 7-coordinate (or higher) without introducing sizable steric repulsions. These combination of factors (and probably others) lead to the high incidence of 6-coordinate Cr3+ complexes.