1. For the following complexes write the systematic name, give the point group, determine the LFSE in units of Dq and P, predict the stability according to the EAN rule, and estimate the spin-only magnetic moment in units of μB. For each complex indicate whether an ionic bonding theory or a covalent bonding theory is more appropriate.
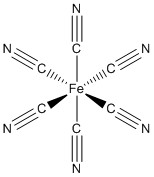
a. [Fe(CN)6]2–
b.
c.
d.
a. [Fe(CN)6]2–
Name: hexacyanoferrate(IV) ion
Point group: Oh
LFSE: d4 in a strong field so LFSE = 16Dq – P
EAN: 4 + 6(2) = 16 e–, probably stable
μ = [2(2+2)]½ = 2.87 μB
Fe4+ is borderline but probably better described with an ionic theory.
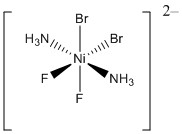
b.
Name: trans-biammine-cis-bibromo-cis-bifluoronickelate(II) ion
Point group: C2v
LFSE: d8 so LFSE = 12Dq
EAN: 8 + 2(2) + 2(2) + 2(2) = 20 e–, not stable
μ = [2(2+2)]½ = 2.87 μB
Ni2+ is better described with an ionic theory.
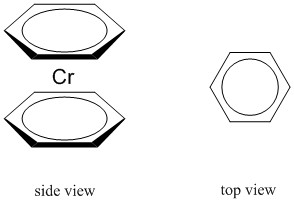
c.
Name: bis-η6-benzenechromium(0)
Point group: D6h
LFSE: d6 in a strong field so LFSE = 24Dq – 2P
EAN: 6 + 2(6) = 18, stable
μ = 0 μB
Cr0 is better described with a covalent theory.
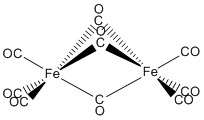
d.
Name: hexacarbonyl-tri-μ-carbonylbiiron(0)
Point group: D3h
LFSE: each Fe is d8 so LFSE = 12Dq
EAN: for each iron - 8 + 6(2) = 20 e– if each bridging CO donates 2 e–; alternately, if each bridging CO donates 1 e– to each Fe, then the count is 8 + 3(2) + 3(1) = 17. Neither count predicts stability. (This is a stable complex: the EAN rule fails here even though it seems like it should work.)
μ = [4(4+2)]½ = 4.90 μB (2 electrons on each Fe). This complex is diamagnetic, μ = 0 μB, another conundrum.
Fe0 is better described with a covalent theory.
2. For the following complexes draw the structure, give the point group, determine the LFSE in units of Dq and P, predict the stability according to the EAN rule, and estimate the spin-only magnetic moment in units of μB. For each complex indicate whether an ionic bonding theory or a covalent bonding theory is more appropriate.
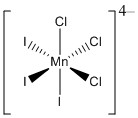
a. fac-trischlorotrisiodomanganate(II) ion
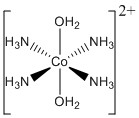
b. trans-tetraamminebiaquacobalt(II) ion
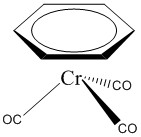
c. η6-benzenetricarbonylchromium(0)
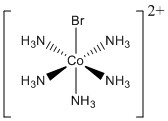
d. pentaamminebromocobalt(III) ion
a. fac-trischlorotrisiodomanganate(II) ion
Structure:
Point group: C3v
LFSE: d5 in a weak field so LFSE = 0Dq
EAN: 5 + 3(2) + 3(2) = 17 e–, not stable
μ = [5(5+2)]½ = 5.92 μB
Mn2+ is better described with an ionic theory.
b. trans-tetraamminebiaquacobalt(II) ion
Structure:
Point group: D4h
LFSE: d7 in a strong field (ammonia is a strong ligand, water is a weak ligand, but there are 4 strong ligands and only 2 weak ligands) so LFSE = 18Dq – P
EAN: 7 + 4(2) + 2(2) = 19 e–, not stable
μ = [1(1+2)]½ = 1.73 μB
Co2+ is better described with an ionic theory.
c. η6-benzenetricarbonylchromium(0)
Structure:
Point group: C3v
LFSE: d6 in a strong field so LFSE = 24Dq – 2P
EAN: 6 + 3(2) + 6 = 18 e–, stable
μ = 0 μB
Cr0 is better described with a covalent theory.
d. pentaamminebromocobalt(III) ion
Structure:
Point group: C4v
LFSE: d6 in a strong field so LFSE = 24Dq – 2P
EAN: 6 + 5(2) + 1(2) = 18 e–, stable
μ = 0 μB
Co3+ is better described with an ionic theory.
3. Predict if the following complexes are Jahn-Teller active or not. If yes, predict the nature of the distortion.
a. [Fe(NH3)6]3+
b. [FeCl6]3–
a. [Fe(NH3)6]3+
Fe3+ is d5 in a strong field, i.e. t2g5, which is Jahn-Teller active and will elongate along the z-axis.
b. [FeCl6]3–
Fe3+ is d5 in a weak field, i.e. t2g3eg2, which is not Jahn-Teller active.
4. Triphenylphosphine is a strong ligand, in part, because it can act as a good backbonding acceptor, similar to CO. Which orbitals on the ligand are responsible for the backbonding? Explain your reasoning.
The lowest lying empty orbitals are the 3d orbitals on the P atom. These have the correct nodal properties to overlap with d orbitals on a metal so a metal can contribute electron density into the P d orbitals.
