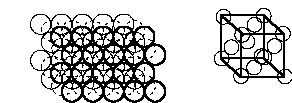
1. Calculate the density of gold using the following information: gold is found in a face centered cubic lattice (fcc) with lattice parameter a = 409 pm (a is the length of the cube edge); the molar mass of gold is 196.97 g/mol; and Avogadro's Number = 6.022×1023. Hint: sketch the structure.
From the lecture notes, an fcc lattice is
There is 1 atom at each corner but only 1/8 is within the cell, giving 8×1/8 = 1 atom contributing to the cell from the corners. There is also 1 atom in each face but only 1/2 within the cell, giving 6×1/2 = 3 atoms from the faces. The total number of atoms in the cell = 1 + 3 = 4.
The density is given by the mass/volume. The mass of the atoms within the cell = (4 atoms per cell)(196.97 g/mol)/ (6.022×1023 mol–1) = 1.308×10–21 g. The volume of a cube = a3 = (4.09×10–8 cm)3 = 6.84×10–23 cm3. Then the density = (1.308×10–21 g)/(6.84×10–23 cm3) = 19.1 g/cm3.
2. Calculate the lattice energy for MgBr2 using the following information: S(Mg) = 148 kJ/mol; IE1(Mg) = 737 kJ/mol; IE2(Mg) = 1476 kJ/mol; V(Br2) (vaporization energy) = 31 kJ/mol; D(Br2) = 193 kJ/mol; EA(Br) = 325 kJ/mol; and ΔH°f = –524 kJ/mol.
The Born-Haber cycle is:
Mg(s) + Br2(l) → MgBr2(s) ΔH°f = –524 kJ/mol
Mg(s) → Mg(g) S(Mg) = 148 kJ/mol
Mg(g) → Mg+(g) IE1(Mg) = 737 kJ/mol
Mg+(g) → Mg2+(g) IE2(Mg) = 1476 kJ/mol
Br2(l) → Br2(g) V(Br2) = 31 kJ/mol
Br2(g) → 2 Br(g) D(Br2) = 193 kJ/mol
2 Br(g) → 2 Br–(g) –2×EA(Br) = –2×325 kJ/mol = –650 kJ/mol
Mg2+(g) + 2 Br(g) → MgBr2(s) –Elat
Then Elat = –ΔH°f + IE1(Mg) + IE2(Mg) + V(Br2) + D(Br2) – 2×EA(Br) = 524 + 148 + 737 + 1476 + 31 + 193 – 650 = 2459 kJ/mol.
3. Metal oxides can be semiconductors because lattice vacancies can exist. These vacancies originate if the metal can attain multiple oxidation states by a low energy oxidation or reduction. Based on this principle, predict whether WO3 is an n-type semiconductore, a p-type semiconductor, or neither. Explain your reasoning. A Latimer diagram for W is given below.
WO3 → –0.029 W2O5 → –0.031 WO2 → –0.119 W
In WO3 the oxidation state of W is +6 and is easily reduced to the +5 state (E°red = –0.029 V). This means that the a small amount of the W could be in the +5 state if there are vacancies at O2– sites (to maintain charge balance). Since W5+ is more negative than W6+, the oxide will be an n-type semiconductor.
4. The conjugate base of boric acid (H3BO3) is B(OH)4– in aqueous solution. Write the balanced Brønsted-Lowry reaction of boric acid with water.
The balanced reaction is:
H3BO3(aq) + 2 H2O(l) →← H3O+(aq) + B(OH)4–(aq)
5. Write the balanced reaction for the disproportionation of HMnO4– into MnO4– and Mn2+.
The balanced reaction is:
oxidation; HMnO4–(aq) → MnO4–(aq) + H+(aq) + e–
reduction: HMnO4–(aq) +7 H+(aq) + 4 e– → Mn2+(aq) + 4 H2O(l)
net: 5 HMnO4–(aq) +3 H+(aq) → 4 MnO4–(aq) + Mn2+(aq) + 4 H2O(l)
