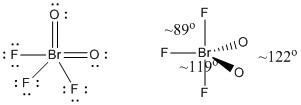1. Write the electron configuration (using rare gas notation for closed shells) and the ground state Term Symbol for the following: a) Sc; b) Sc+; c) Sc2+; d) Sc3+; e) Sc–.
a) Sc
[Ar]4s23d1
Only the 3d electron contributes to the term symbol: L = 2 and S = ½ giving 2D
b) Sc+
[Ar]3d2
L = 3 and S = 1 giving 3F
c) Sc2+
[Ar]3d1
L = 2 and S = ½ giving 2D
d) Sc3+
[Ar]
L = 0 and S = 0 giving 1S
d) Sc–
[Ar]4s23d2
L = 3 and S = 1 giving 3F
2. Write the Lewis dot structure, give the formal charges on all atoms, predict the molecular geometry, estimate of all bond angles, and give the likely hybrid orbital for the following: a) BrO2–; b) BrO3–; c) BrO2F3.
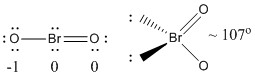
a) BrO2–
Lewis Structure:
Formal charges are given on the Lewis Structure
Structure: bent planar with a bond angle of ~107°
Hybrid orbital on Br: sp3
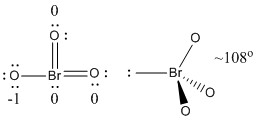
b) BrO3–
Lewis Structure:
Formal charges are given on the Lewis Structure
Structure: pyramidal with bond angles O-Br-O ~108°
Hybrid orbital on Br: sp3
c) BrO2F3
Lewis Structure:
Formal charges are given on the Lewis Structure
Structure: trigonal bipyramidal with bond angles shown in the figure
Hybrid orbital on Br: dsp3
3. The Absolute Hardness of an atom is defined as η = ½(IP – EA), IP is the ionization potential and EA is the electron affinity. Predict the periodic trends of η and provide reasoning for your prediction.
For nearly all atoms IP >> EA, so η will follow the periodic trends of IP: increasing as one moves right on the Periodic Table (following Z*) and decreasing slightly as one moves down the Periodic Table as the atomic radius increases.
4. Cr2 has an electron configuration of σ2π4δ4δ*2. What is the bond order and how many unpaired spins are predicted? Would you expect Cr2 to absorb light in the visible region of the spectrum? Why or why not?
The bond order = ½(2 + 4 + 4 – 2) = 4 with 2 unpaired spins (since there are 2 δ orbitals there must also be 2 δ* orbitals, which each have one electron based on Hund's rules). The side by side overlap of d orbitals to form δ orbitals is poor so that the splitting between the δ and δ* orbitals will be small. This suggests that the energy required to move an electron from the HOMO to the LUMO is also small, which predicts an absorption in the visible part of the spectrum.
