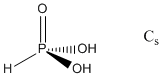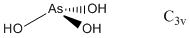1. The sphalerite and wurtzite forms of ZnS are structurally similar: in sphalerite the Zn2+ ions occupy Td holes in a ccp lattice and in wurtzite the Zn2+ ions occupy Td holes in a hcp lattice. Use the Born-Landé equation to predict the thermodynamically more stable form of ZnS. Possibly helpful information: n = 9 for ZnS; r+ = 75 pm; r– = 170 pm; Noe2/4πεo = 1.389×10–4 J m/mole.
The Born-Landé estimates the lattice energy as Elat = –[Noe2Z+Z–A/4πεodo](1 – 1/n), where A is the Madelung constant, Z+ = +2, Z– = –2, do = r+ + r– = 75 + 170 = 245 pm, and the other values are given in the question.
For sphalerite, A = 1.638 so Elat = –[(1.389×10–4 J m/mole)(+2)(–2)(1.638)/ (245×10–12 m)](1 – 1/9) = 3302 kJ/mol.
For wurtzite, A = 1.641 so Elat = –[(1.389×10–4 J m/mole)(+2)(–2)(1.641)/ (245×10–12 m)](1 – 1/9) = 3308 kJ/mol.
Based on these lattice energies, the wurtzite structure is predicted to be slightly more stable.
In fact, the sphalerite structure is the ground state. The calculated values are so close that more precise information about the ionic distances and the Born exponent would be needed to accurately predict the relative energies of the two structures.
2. For H3PO3, pKa1 ~ 2 and for H3AsO3, pKa1 ~ 9. Use Pauling's rules to suggest a structure for each acid. Find the point group for each acid based on your structure.
Pauling's rule says that pKa1 ~ 8 – 5p where p is the number of oxo (double bonded) type oxygen atoms in the structure. Thus, for H3PO3 this implies 1 oxo-type O and for H3AsO3 0 oxo-type O. The structures and point groups are:
3. Predict the products and balance the equation for the following reactions:
a. SO3(g) + H2O(l)
b. Na2O(s) + H2O(l)
c. [Fe(SCN)6]3–(aq) + NH3(g)
a. SO3(g) + H2O(l) → HSO4–(aq) + H+(aq) (covalently bonded acidic oxide)
b. Na2O(s) + H2O(l) → 2 Na+(aq) + 2 OH–(aq) (ionically bonded oxide)
c. [Fe(SCN)6]3–(aq) + 6 NH3(g) → [Fe(NH3)6]3+(aq) + 6 SCN–(aq) (Lewis acid-base substitution reaction with the harder ammonia displacing the softer thiocyanide ion to bond to the hard acid, Fe3+)
4. Using the Latimer Diagram for Re in a basic solution, find the standard reduction potential for the conversion of ReO2 to Re. Write the balanced half-reaction.
The 4-electron reduction of ReO2 is found by the weighted average of the 1-electron reduction and the 3-electron reduction given in the Latimer Diagram: Eo = [(1)(–1.25) + (3)(–0.33)]/(1 + 3) = –0.56 V.
The balanced equation in acidic solution would be:
ReO2(s) + 4 H+(aq) + 4 e– → Re(s) + 2 H2O(l)
Neutralizing the H+ with OH– (added to both sides of the equation) and consolidating water molecules gives:
ReO2(s) + 2 H2O(l) + 4 e– → Re(s) + 4 OH–(aq)
