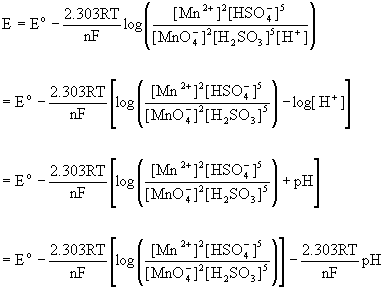1. Which of the following schemes for the repeating pattern of close-packed planes are not ways of generating close-packed lattices? (a) ABCABC ... (b) ABAC ... (c) ABBA ... (d) ABCBC ... (e) ABABC... (f) ABCCB ... Explain.
(a) ABCABC ... is close-packed - this is the ccp lattice.
(b) ABAC ... is close-packed - the fourth layer (C) is just the other alternative for the placement of the B layer.
(c) ABBA ... is not close-packed - the adjacent B layers are not sphere to crevice.
(d) ABCBC ... is close-packed - this is similar to case (b).
(e) ABABC ... is close-packed - this is the same as (d).
(f) ABCCB ... is not close-packed - the adjacent C layers are not sphere to crevice.
2. The Coulombic attraction of nearest-neighbor cations and anions accounts for the bulk of the lattice enthalpy of an ionic compound. With this fact in mind, estimate the order of increasing lattice enthalpy of (a) MgO, (b) NaCl, (c) AlN, all of which crystallize in the rock-salt structure. Give your reasoning.
The nearest neighbor Coulombic attraction depends upon the ion charges and the distance between the ions. The changes in distance between ions is relatively small compared to the unit changes found in the ion charges, so MgO (+2, –2) has a roughly 4× larger lattice enthalpy than NaCl and AlN (+3, –3) has roughly 9× the lattice enthalpy of NaCl. Thus, the predicted order of lattice enthalpies is: NaCl < MgO < AlN.
3. Predict whether the equilibrium constants for the following reactions should be greater than 1 or less than 1. Explain.
a) CdI2(s) + CaF2(s) → ← CdF2(s) + CaI2(s)
b) [CuI4]2–(aq) + [CuCl4]3–(aq) → ← [CuCl4]2–(aq) + [CuI4]3–(aq)
c) NH2–(aq) + H2O(l) → ← NH3(aq) + OH–(aq)
<(a) Use hard-soft acid base theory to approach the problem:
CdI2(s)+CaF2(s) →← CdF2(s)+CaI2(s)
SA-SBHA-HB SA-HBHA-SB
The preferred direction is reactants so the equilibrium constant is less than 1.
(b) Again, use hard-soft acid base theory to approach the problem:
[CuI2]2–(aq)+ [CuCl4]3–(aq) →← [CuCl4]2–(aq)+ [CuI4]3–(aq)
HA-SBSA-HB HA-HBHA-HB
The preferred direction is products so the equilibrium constant is greater than 1.
(c) Since the acid portion is the same in each of these, HSAB theory is less useful. Recall that water can either donate or accept a hydrogen ion in water but ammonia is a very poor hydrogen ion donor, meaning that amide ion is a very strong base:
NH2–(aq)+ H2O(l) →← NH3(aq)+ OH–(aq)
The preferred direction is products so the equilibrium constant is greater than 1./p>
4. Balance the following redox reaction in acid solution: MnO4–(aq) + H2SO3(aq) → Mn2+(aq) + HSO4–(aq). Predict the qualitative pH dependence on the net potential for this reaction (i.e. increases, decreases, remains the same).
Split the reaction into the two half-reactions and balance each separately:
MnO4–(aq) + 8 H+(aq) + 5 e– → Mn2+(aq) + 4 H2O(l)
H2SO3(aq) + H2O(l) → HSO4–(aq) + 3 H+(aq) + 2 e–
so the net reaction is:
2 MnO4–(aq) + 5 H2SO3(aq) + H+(aq) → 2 Mn2+(aq) + 5 HSO4–(aq) + 3 H2O(l)
Since hydrogen ion is a reactant, an increase in pH lowers the hydrogen ion concentration, driving the reaction towards reactants, thereby decreasing the net potential.
This can be thought of in terms of the Nernst equation, as well:
That is, increasing the pH subtracts from the standard potential so the net potential decreases with increasing pH.
5. Draw a Frost diagram for mercury in acid solution. Comment on the tendency of any of the species to act as an oxidizing agent, a reducing agent, or to undergo disproportionation.
There are 3 available oxidation states: 0, 1, 2
For the +1 oxidation state N = +1 and E° = 0.796 so NE° = +0.796 V
For the +2 oxidation state N = +2 and E° = (0.911 + 0.796)/2 = 0.854 V so NE° = +1.708 V
The Frost diagram then is:
Both Hg2+ and Hg22+ should be able to act as oxidizing agents (the reduction is favorable) but Hg22+ should not undergo disproportionation.
6. Calculate the lattice energy (in units of kJ/mol) for ZnO in the wurtzite structure using the Born-Landé equation and using a Born-Haber cycle. Compare the two answers and comment on any differences. Useful data: the Born exponent, n, = 8; the sublimation energy of zinc = 130.4 kJ/mol; and the standard heat of formation of zinc(II) oxide = –350.5 kJ/mol. Other data can be found in the textbook.
For the theoretical calculation using the Born-Landé equation:
Elat = –[(N0Z+Z–e2A)/(4πε0d0)](1 – 1/n)
N0 = 6.022×1023
Z+ = +2
Z– = –2
e = 1.602×10–19
A = 1.641 for the wurtzite structure
4πε0 = 1.113×10–10
d0 = 60 + 138 = 198 pm (for coordination number = 4) = 1.98×10–10 m
n = 8
Elat = –[(6.022×1023)(2)(–2)(1.602×10–19)2(1.641)/ (1.113×10–10)(1.98×10–10)](1 – 1/8) = 4027900 J/mol = 4028 kJ/mol
Using the Born-Haber cycle:
Zn(s) + ½ O2(g) → ZnO(s) ΔH°f = –350.5 kJ/mol
Zn(s) → Zn(g) S = 130.4 kJ/mol
Zn(g) → Zn+(g) IE1 = (9.393 eV)(96.485 kJ/mol/eV) = 906.3 kJ/mol
Zn+(g) → Zn2+(g) IE2 = (17.96 eV)(96.485 kJ/mol/eV) = 1733 kJ/mol
½ O2(g) → O(g) ½D = ½(497) = 248.5 kJ/mol
O(g) → O–(g) EA1 = 141 kJ/mol
O–(g) → O2–(g) EA2 = –780 kJ/mol
Zn2+(g) + O2–(g) → ZnO(s) –Elat
S + IE1 + IE2 + ½D – EA1 – EA2 – Elat – ΔH°f = 0
Elat = 130.4 + 906.3 + 1733 + 248.5 – 141 – (–780) – (–350.5) = 4008 kJ/mol
The agreement between theory and experiment is remarkable!
