1. For each of the following, draw the structure, determine the point group, find the LFSE (in terms of Dq and P), estimate the magnetic moment in terms of Bohr-Magnetons, predict the stability based on the EAN rule, and indicate if the complex will be Jahn-Teller active. If the complex is Jahn-Teller active, indicate the nature of the distortion. Indicate which bonding theory is the better choice for each species.
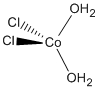
a. diaquadichlorocobalt(II)
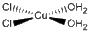
b. cis-diaquadichlorocopper(II)
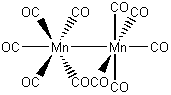
c. decacarbonyldimanganese(0) (deca = 10)
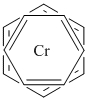
d. bis-(η6-benzene)chromium(0)
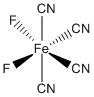
e. cis-tetracyanodifluoroferrate(II) ion
a. diaquadichlorocobalt(II)
Structure:
Point Group: C2v
LFSE: d9 in an Oh field, t2g6eg3: 6Dq
Unpaired Spins: 1
Magnetic Moment: 3.87 μB
EAN: 7[Co2+] + 2(2)[H2O] + 2(2)[Cl–] = 15, not stable
Jahn-Teller Active: No
Distortion: none
Better Theory: ionic (Co2+)
b. cis-diaquadichlorocopper(II)
Structure:
Point Group: C2v
LFSE: d7 in a Td field, e4 t23: 12Dqt
Unpaired Spins: 3
Magnetic Moment: 1.73 μB
EAN: 9[Cu2+] + 2(2)[H2O] + 2(2)[Cl–] = 17, not stable
Jahn-Teller Active: Yes
Distortion: elongation
Better Theory: ionic (Cu2+)
c. decacarbonyldimanganese(0) (deca = 10)
Structure:
Point Group: D4d
LFSE: d7 in a strong Oh field, t2g6eg1: 18Dq – P
Unpaired Spins: 0 (because of the covalent Mn-Mn bond)
Magnetic Moment: 0 μB
EAN: 7[Mn0] + 5(2)[CO] + 1[Mn-Mn bond] = 18, stable
Jahn-Teller Active: Yes
Distortion: either
Better Theory: covalent (Mn0)
d. bis-(η6-benzene)chromium(0)
Structure:
Point Group: D6d
LFSE: d6 in a strong Oh (sort of) field, t2g6: 24Dq – 2P
Unpaired Spins: 0
Magnetic Moment: 0 μB
EAN: 6[Cr0] + 2(6)[η6-benzene] = 18, stable
Jahn-Teller Active: No
Distortion: none
Better Theory: covalent (Cr0)
e. cis-tetracyanodifluoroferrate(II) ion
Structure:
Point Group: C2v
LFSE: d6 in a strong Oh field, t2g6: 24Dq – 2P
Unpaired Spins: 0
Magnetic Moment: 0 μB
EAN: 6[Fe2+] + 4(2)[CN–] + 2(2)[F–] = 18, stable
Jahn-Teller Active: No
Distortion: none
Better Theory: ionic (Fe2+)
2. For each of the following, give the systematic name, determine the point group, find the LFSE (in terms of Dq and P), estimate the magnetic moment in terms of Bohr-Magnetons, predict the stability based on the EAN rule, and indicate if the complex will be Jahn-Teller active. If the complex is Jahn-Teller active, indicate the nature of the distortion. Indicate which bonding theory is the better choice for each species.
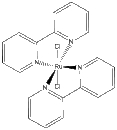
a. trans-Ru(bpy)2Cl2
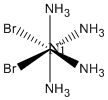
b. cis-Ni(NH3)4Br2 (ignore H atoms when determining the point group)
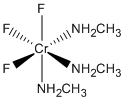
c. fac-Cr(CH3NH2)3F3 (ignore H atoms when determining the point group)
d. Mo(CO)6
e. Mn(η5-cp)(CO)3
a. trans-Ru(bpy)2Cl2
Name: trans-bis(2,2'-bipyridine)dichlororuthenium(II)
Structure:
Point Group: D2h
LFSE: d6 in a strong Oh field, t2g6: 24Dq – 2P
Unpaired Spins: 0
Magnetic Moment: 0 μB
EAN: 6[Ru2+] + 2(4)[bpy] + 2(2)[Cl–] = 18, stable
Jahn-Teller Active: No
Distortion: none
Better Theory: ionic (Ru2+)
b. cis-Ni(NH3)4Br2
Name: cis-tetraamminedibromonickel(II)
Structure:
Point Group: C2v
LFSE: d8 in an Oh field, t2g6eg2: 12Dq
Unpaired Spins: 2
Magnetic Moment: 2.83 μB
EAN: 8[Ni2+] + 4(2)[NH3] + 2(2)[Br–] = 20, not stable
Jahn-Teller Active: No
Distortion: none
Better Theory: ionic (Ni2+)
c. fac-Cr(CH3NH2)3F3
Name: mer-trifluorotrismethylaminechromium(III)
Structure:
Point Group: C3v
LFSE: d3 in an Oh field, t2g3: 12Dq
Unpaired Spins: 3
Magnetic Moment: 3.87 μB
EAN: 3[Cr3+] + 3(2)[NH3] + 3(2)[F–] = 15, not stable
Jahn-Teller Active: No
Distortion: none
Better Theory: ionic (Cr3+)
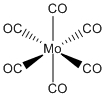
d. Mo(CO)6
Name: hexacarbonylmolybdenum(0)
Structure:
Point Group: Oh
LFSE: d6 in a strong Oh field, t2g6: 24Dq – 2P
Unpaired Spins: 0
Magnetic Moment: 0 μB
EAN: 6[Mo0] + 6(2)[CO] = 18, stable
Jahn-Teller Active: No
Distortion: none
Better Theory: covalent (Mo0)
e. Mn(η5-cp)(CO)3
Name: tricarbonyl-η5-cyclopentadienylmanganese(I)
Structure:
Point Group: Cs
LFSE: d6 in a strong Oh field, t2g6: 24Dq – 2P
Unpaired Spins: 0
Magnetic Moment: 0 μB
EAN: 6[Mn1+] + 1(6)[η5-cp] + 3(2)[CO] = 18, stable
Jahn-Teller Active: No
Distortion: none
Better Theory: covalent (Mn1+)
