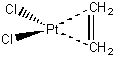1. For each of the following, draw the structure, determine the point group, find the LFSE (in terms of Dq and P), estimate the magnetic moment in terms of Bohr-Magnetons, predict the stability based on the EAN rule, and indicate if the complex will be Jahn-Teller active. If the complex is Jahn-Teller active, indicate the nature of the distortion.
a. dichloro-η²-etheneplatinum (II).
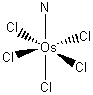
b. pentachloronitridoosmate(VI) ion.
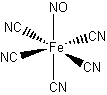
c. pentacyanonitrosylferrate(III) ion. (Assume all of the ligands are linear with respect to the metal.)
a. dichloro-η²-etheneplatinum (II).
Structure:
Point group: C2v
LFSE: Pt(II) is d8 so the LFSE = 12Dq (assuming the Oh electronic structure).
Magnetic moment: d8 has 2 unpaired spins so μ = [2(2+2)]½ = 2.83 μB
EAN rule: d8 contributes 8 electrons, each chloride contributes 2 electrons, and the ethene contributes 2 electrons (from the π bond) for a total of 14 electrons, which is not predicted to be stable.
Jahn-Teller: d8 is not Jahn-Teller active.
b. pentachloronitridoosmate(VI) ion.
Structure:
Point group: C4v
LFSE: Os(VI) is d2 so the LFSE = 8Dq.
Magnetic moment: d2 has 2 unpaired spins so μ = [2(2+2)]½ = 2.83 μB
EAN rule: d2 contributes 2 electrons, each chloride contributes 2 electrons, and the nitride contributes 2 electrons for a total of 14 electrons, which is not predicted to be stable.
Jahn-Teller: d2 is Jahn-Teller active and should exhibit an axial elongation.
c. pentacyanonitrosylferrate(III) ion.
Structure:
Point group: C4v
LFSE: Fe(III) is d5 and the cyanide ligand is strong so the LFSE = 20Dq – 2P.
Magnetic moment: d5 in a strong field has 1 unpaired spin so μ = [1(1+2)]½ = 1.73 μB
EAN rule: d5 contributes 5 electrons, each cyanide contributes 2 electrons, and the NO contributes 2 electrons for a total of 17 electrons, which is not predicted to be stable.
Jahn-Teller: d5 in a strong field is Jahn-Teller active and should exhibit an axial elongation.
2. A CO ligand can often be removed from carbonyl complexes using light. Explain this observation in terms of molecular orbital theory for an octahedral complex.
Upon overlap with the ligand orbitals, the d electrons become π (t2g) and σ* (eg) orbitals. Light excites an electron from a π orbital in the antibonding σ* orbital, which reduces the bond order enough that a M-CO bond is broken.
3. PF3 has a similar position in the spectrochemical series as CO. Both ligands act similarly: the donate electrons to the metal through a lone pair and accept electrons from metal π orbitals. Explain how PF3 can act as a σ donor and a π acceptor in metal complexes.
The Lewis structure for PF3 has a lone pair on the P atom - :PF3, which accounts for the σ donation from the ligand to the metal. The valence orbitals for PF3 are 3s and 3p, which are using in the bonding of the ligand, but there are relatively low lying 3d orbitals that are empty and can act as acceptors for electrons from the metal, similar to the π* orbitals in CO. The high electronegativity of F on the PF3 also helps attract electron density to the ligand, which serves to increase the bond strength between the metal and the phosphorus.
4. The compound Rh(H)(CO)(PPh3)3 can be used as a hydroformylation catalyst. Draw the structure and indicate how this compound might act catalytically. (PPh3 = triphenylphosphine).
The structure of Rh(H)(CO)(PPh3)3 is
. Note that the bulky triphenylphosphine ligands occupy the least sterically restricted sites, i.e., the equatorial positions.
Since the Rh(I) is 5-coordinate, there is room to add a substrate for further reactivity. The complex is an 18-electron species (Rh(I), d8, and each ligand contributing 2 electrons) so an oxidative addition can accommodate a substrate for further reactivity.
