Chemistry 401
Intermediate Inorganic Chemistry
University of Rhode Island
Fall 2006
Final Exam
All references are to volume 45 of Inorganic Chemistry (2006).
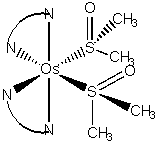
1. N. V. Mockus, J. L. Petersen, and J. J. Rack (pages 8–10) investigated some of the properties of [Os(bpy)2(DMSO)2]2+, where DMSO is (CH3)2S=O (dimethylsulfoxide). DMSO is an ambidentate ligand that, in this complex, bonds in a cis geometry through the S atoms. Name the complex and estimate the N-Os-N, N-Os-S, C-S-C, and C-S-O bond angles.
[Os(bpy)2(DMSO)2]2+ = cis-bis(2,2'-bipyridine)bis(S-dimethylsulfoxide)osmium(II) ion.
The geometry is:
There are several N-Os-N angles: the N-Os-N angle through the chelation is reduced significantly from 90° because of the bite angle of the chelating bpy ligand, perhaps ~80°; the other N-Os-N angles should be closer to 90° or 180°, depending upon the relative orientation of the N atoms.
There are also several N-Os-S angles: the N-Os-S angles in the plane of bpy ligands will be greater than 90°, ~95°, because the N-Os-N angle is reduced by chelation; the other N-Os-S angles should be closer to the ideal values of 90° or 180°, depending upon the relative orientation.
The S center is tetrahedral but the bulky Os substituent and the S=O electron density will reduce the C-S-C angle significantly to ~100°.
The bulky Os substituent will dominate the C-S-O angle, as well, but to a lesser degree because of the electron density in the S=O bond, so the C-S-O angle is ~105°.
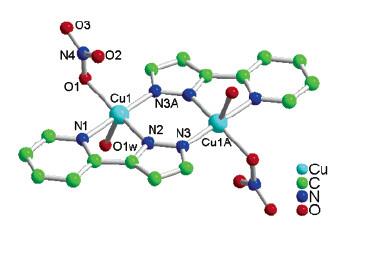
2. T.-L. Hu, J.-R. Li, C.-S. Liu, X.-S. Shi, J.-N. Zhou, X.-H. Bu, and J. Ribas (pages 162–173) studied the complex shown below. Find the point group for the complex. The measured magnetic moment at room temperature is 2.37 μB. Suggest an explanation for this value. Hint: both copper atoms are in the +2 oxidation state.
The only symmetry element present in the complex is an inversion center, so the point group is Ci
Cu2+ is d9, which has 1 unpaired spin. Since there are 2 Cu2+ ions in the compound, there should be a total of 2 unpaired spins, predicting a spin-only magnetic moment of u = [2(2+2)]½ = 2.83 uB. The observed value is significantly smaller. The other extreme is that the magnetic moment is reported per Cu2+ ion, so μ = [1(1+2)]½ = 1.73 μB. This value is much smaller than observed. The best explanation is that the two Cu2+ ions are interacting in some fashion to cause a slight pairing of the spins (this is called an antiferromagnetic interaction).
3. M. Finze, E. Bernhardt, H. Willner, and C. W. Lehman (pages 669–678) examined the reactivity of (CF3)3BCO. Predict the reaction product for the following reaction and explain your reasoning:
(CF3)3BCO + NH3 → ?
(CF3)3BCO is a Lewis acid-base complex, perhaps better written as (CF3)3B:CO:. Thus, a reasonable prediction for the reactivity is for the NH3 to subsitute for the CO. Thus,
(CF3)3BCO + NH3 → (CF3)3B:NH3 + CO
In fact, the reaction is not a simple substitution, rather an addition reaction occurs:
(CF3)3BCO + NH3 → (CF3)3B-(C=O)-NH3
which is then followed by subsequent reactions.
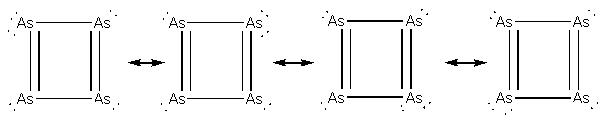
4. F. Kraus, T. Hanauer, and N. Korber (pages 1117–1123) calculated that As42– should be aromatic. Draw the Lewis dot structure for this ion and explain how aromaticity could be attained.
The Lewis structure can be represented by four different resonance structures:
Aromaticity arises from two double bonds and the lone pair of electrons that can reside on any of the As atoms. The Hückel rule is satisfied: 6 electrons in a planar ring structure.
5. C. Chazel, M. Ménétrier, L. Croguenne, and C. Delmes (pages 1184–1191) synthesized LixNiO2, where x = 0.25. Assign the formal oxidation states of each atom in this compound. They report that the electrical conductivity is thermally activated. Does this suggest that LixNiO2 is a metal or a semiconductor? Why?
Li+ has an oxidation state of +1, O2– has an oxidation state of –2, so the Ni must have a formal oxidation state of +3.75, i.e., a mixture of 75% +4 and 25% +3.
The fact that the electrical conductivity is thermally activated means that Li0.25NiO2 is a semiconductor. Li+ can be thought of as a dopant, although at much higher levels than typically found in semiconductors.
6. H. D. B. Jenkins and L. Glasser (pages 1754–1756) proposed a simple method for finding lattice energies for 1:1 salts with Z+ = +2 and Z– = –2 using only the ionic volume:
Elat = 8(119/V1/3 + 60)
where V is the ionic volume in units of nm3 and Elat is in kJ/mol. In one of the class assignments it was found that the lattice energy for ZnO (wurtzite structure) was 4008 kJ/mol using a Born-Haber cycle. Calculate the lattice energy using Jenkins & Glasser's formula and compare the result to the experimental value. Explain any discrepancies.
The ionic radius of Zn2+ (CN = 4) is 75 pm and the ionic radius of O2– (CN = 4) is 124 pm. Thus, the 'compound' radius is 75 + 124 = 199 pm = 0.199 nm. This gives a volume of 4πr3/3 = 4π(0.199)3/3 = 0.0330 nm3
Using this in the given formula gives the lattice energy to be Elat = 8(119/(0.0330)1/3 + 60) = 3450 kJ.
The Jenkins/Glasser calculation is ~14% low compared to the experimental value. For the simplicity of the method, the calculated result is not too bad, but the error is still pretty large. Better ionic radii might account for some of the error, but mostly the method overlooks some of the contributing energies.
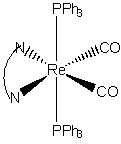
7. J. L. Smithback, J. B. Helms, E. Schutte, S. M. Woessner, and B. P. Sullivan (pages 2163–2174) used 2,2'-bipyridine-cis-bis(carbonyl)-trans-bis(triphenylphosphine)rhenium(I) as a reagent in a synthesis. Draw the structure of this ion, determine if it is stable by the EAN rule, and predict the magnetic moment.
The structure is:
Re+ is d6, each N on the bpy ligand donates 2 electrons, each CO donates 2 electrons, and each P on the triphenylphosphines donate 2 electrons. The total is 6 + 2(2) + 2(2) + 2(2) = 18, so the complex is expected to be stable.
All of the ligands are strong field so this should be a low spin complex with 0 unpaired spins and μ = 0 μB.
8. J.-J. Wang, C. Tessier, and R. H. Holm (pages 2979–2988) discuss the reaction of selenate ion with a Mo complex, as shown below:
SeO42–(aq) + [Mo(OH)(S2C2(CH3)2)2]1–(aq) → SeO32–(aq) + [Mo(O)(OH)(S2C2(CH3)2)2]1–(aq)
where S2C2(CH3)22– (–S-C(CH3)=C(CH3)-S–) is a chelating ligand. Balance the reaction and indicate which species are oxidized and reduced. Would you expect this oxidation-reduction reaction to be inner sphere or outer sphere. Explain your reasoning.
The reaction is balanced as shown.
The Se is reduced from +6 to +4 while the Mo is oxidized from +4 to +6.
The Mo complex is coordinately unsaturated: the chelating S2C2(CH3)22– ligands occupy 4 sites and the hydroxide group occupies a fifth site. Thus, this reaction is expected to be inner sphere, where an oxygen atom from the selenate ion coordinates to the sixth site on the Mo complex, which is followed by an O atom transfer.
9. Ellis (pages 3167–3186) in a review paper cites Ni(CO)4, [Co(CO)4]–, and [Fe(CO)4]2– as examples of interesting organometallic compounds. Predict the structure and stability of each of these complexes. Give the formal oxidation state of the metal in each case.
All of these complexes are tetrahedral:
All of the metals are d10 and each CO ligand contributes 2 electrons. Thus, the total electron count is 10 + 4(2) = 18 for each complex and all of these are expected to be stable.
The formal oxidation states are Ni0, Co–1, and Fe–2. The formally negative oxidation states on the metal atoms is what makes them interesting.
10. R. Beaulac, P. L. W. Tregenna-Piggott, A.-L. Barra, H. Weihe, D. Luneau, and C. Weber (pages 3399–3407) characterized the compound [V(urea)6](ClO4)3, where urea is H2N(C=O)NH2, which coordinates through the O atom. They find the lowest spin allowed transition in the optical spectrum to be at ~16000 cm–1. Find 10Dq (in units of cm–1) and predict the geometry around the V atom. Would you expect urea to be a weak field or strong field ligand? Explain your reasoning.
V3+ is d2 so the lowest energy spin-allowed optical transition is 8Dq. This means that Dq ~ 2000 cm–1 and 10Dq ~ 20000 cm–1.
The d2 configuration is Jahn-Teller active, so the geometry of the complex is expected to be a distorted octahedron, with axial elongation favored to remove the degeneracy. (In fact, the complex distorts along the C3 axis, not the C4 axis.)
Since the d2 configuration does not have high-spin or low-spin options, the ligand strength must be estimated from the magnitude of 10Dq. Examination of Table 19.1 in the textbook suggests that a ligand with 10Dq of ~ 20000 cm–1 is probably strong field, but this conclusion is tentative since Table 19.1 does not include any examples of d2 ions.