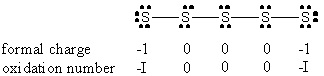Chemistry 401
Intermediate Inorganic Chemistry
University of Rhode Island
Fall 2000
Final Exam
All references are to articles from Inorganic Chemistry, 2000, 39.
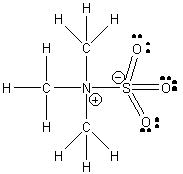
1. D. L. Fiacco, A. Toro, and K. R. Leopold (p. 37-43) investigated the gas phase structure of the Lewis acid/base complex (CH3)3N–SO3. Draw the Lewis dot structure for this compound, estimate the C-N-S and N-S-O bond angles (± 2°), and indicate the hybridization at the N and S atoms.
The C-N-S angle should be very close to the ideal tetrahedral angle, 109°. The high electron density in the S=O bonds will cause repulsion between the S=O groups, thereby increasing the O-S-O angle and reducing the N-S-O angle to ~107°. Both the S and N are sp3 hybridized.
2. M. M. Hosain and K. Matsumoto (p. 247-250) used the pentasulfide anion, S52–, as a tridentate ligand in the complex Ru(P(OCH3)3)3S5. Draw the Lewis dot structure of the pentasulfide anion (assume the octet rule is obeyed and there is a linear connectivity between sulfur atoms) and indicate the formal charge and formal oxidation number on each S atom. Name the metal complex. P(OCH3)3 is a neutral ligand named trimethylphosphite.
This implies that pentasulfide is a dianion.
Pentasulfide most likely binds to a metal from the formally negative sites at the ends and, to behave as a tridentate ligand, one of the central S atoms (experimentally found to be the 2nd S atom along the chain). This constrains the geometry of the metal complex so that only the fac isomer can form. Thus, the name of the complex is: fac-pentasulfide-tris-(trimethylphosphite)ruthenium(II)
3. R. Churland, U. Frey, F. Metz, and A. E. Merbach (p. 302-307) prepared the complexes [M(CO)2Cl2]– (M = Rh, Ir). Are these complexes expected to be stable by the effective atomic number rule? Why or why not? If not, what reactivity would you anticipate?
[Rh(CO)2Cl2]–: Rh+ is d8; CO is a 2-electron donor and Cl– is also a 2-electron donor so the total electron count is 8 + 2(2) + 2(2) = 16, probably stable. [Ir(CO)2Cl2]– is identical (Ir is just below Rh on the Periodic Table).
4. B. Schüpp, P. Heines, A. Savin, and H.-L. Keller (p. 732-735) studied the pressure induced redox reaction: Cs2PdI4–I2 → Cs2PdI6. Which atom is oxidized and which atom is reduced? The high-pressure phase (Cs2PdI6) is a close-packed structure (face-centered cubic); which ion establishes the lattice packing and which atom fills holes? Why?
Cs+2Pd2+I –4–I02 → Cs+2Pd4+I –6
The Pd atom is oxidized and the solvated I atom is reduced.
The octahedral complex PdI62– is large and spherical, so should be expected to form the lattice. The smaller Cs+ ion fills holes.
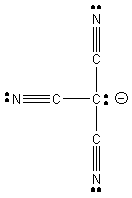
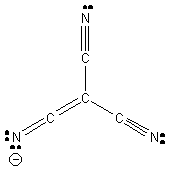
5. J. L. Manson, E. Ressouche, and J. S. Miller (p. 1135-1141) found that the room temperature magnetic moment of Cr(C(CN)3)2 was 4.7 bohr-magnetons. Is this complex high spin or low spin? To deduce the charge on tricyanomethide, draw the Lewis dot structure assuming that all atoms maintain octets. Tricyanomethide is found to have a D3h symmetry. Is this consistent with your Lewis dot structure? Why or why not? If it is not consistent with your Lewis dot structure, draw a Lewis dot structure that is consistent with D3h symmetry.
This is one possible Lewis dot structure that maintains octets on all atoms, implying that the anion has a –1 charge. However, this is not consistent with a D3h structure; the structure shown would be C3v. Another Lewis structure (1 of 3 identical resonance forms) consistent with the D3h structure is:
Since the ligand is a monoanion, then the Cr must be in the +2 oxidation state, which is a d4 electron configuration. For a high spin case (4 unpaired spins) the magnetic moment is expected to be ~[4(4+2)]½ = 4.9 bohr-magnetons; for the low spin case (2 unpaired spins) the magnetic moment is expected to be ~[2(2+2)]½ = 2.8 bohr-magnetons. The complex must be high spin.
6. B. Saha and D. M. Stanbury (p. 1294-1300) studied the reaction [Ru(bpy)3]2+ + Cl2 → [Ru(bpy)3]3+ + Cl–. Balance the reaction and estimate E° for this reaction under standard acidic conditions. Would you expect the reaction mechanism to be inner sphere or outer sphere? Why? bpy = 2,2'-bipyridine.
Oxidation:
[Ru(bpy)3]2+ → [Ru(bpy)3]3+ + e–
E°red = 1.53 V so E°ox = –1.53 V (Shriver and Atkins, Appendix 2, page 706)
Reduction:
Cl2 + 2 e– → 2 Cl–
E°red = 1.358 V (Shriver and Atkins, Appendix 2, page 699)
Net:
2 [Ru(bpy)3]2+ + Cl2 → 2 [Ru(bpy)3]3+ + 2 Cl–
E° = E°red + E°ox
E° = 1.358 – 1.53 = –0.17 V
The reaction is probably outer sphere because the metal complex has a filled coordination sphere.
7. O. Gourdon, J. Hanko, F. Boucher, V. Petricek, M.-H. Whangbo, M. G. Kanatzidis, and M. Evain (p. 1398-1409) calculated the electronic band structure for K1/3Ba2/3AgTe2. Would you expect this material to be a p-type or n-type semiconductor? Hint: assume that the metal ions exist in their most common oxidation states.
K1/3Ba2/3AgTe2: the hint tells us that the metal oxidation states are K+, Ba2+, and Ag+, requiring the Te to be –[(1/3)(+1) + (2/3)(+2) + (+1)]/2 = –4/3. Since the natural oxidation state of Te is Te2–, there is an excess of positive charge on the Te atoms, implying the the compound is a p-type semiconductor.
8. R. P. Singh and J. M. Shreeve (p. 1787-1789) synthesized (C6F13)2P(O)OH. Would you expect this acid to have a pKa higher or lower than phosphoric acid? Briefly explain your reasoning.
Phosphoric acid is P(O)(OH)3 with pKa1 estimated to be ~5 – 3 = 2, using Pauling's rules. Pauling's rules are based on electronegativity arguments, i.e., the X=O group is highly electronegative, thereby drawing electron density away from the rest of the molecule and making any OH bonds more acidic. The C6F13 group has a huge number of F atoms attached, thus could be expected to be even more electronegative than the oxo group. Thus, (C6F13)2P(O)OH is predicted to be a stronger acid than phosphoric acid and have a lower pKa.
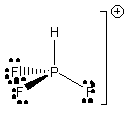
9. R. Küster, T. Drews, and K. Seppelt (p. 2784-2786) prepared PF3H+. Draw the Lewis dot structure, predict all of the bond angles to ± 2°, indicate the hybridization on the P atom, and give the point group for this cation.
The electronegative F atoms will draw electron density, leading to repulsion between the P-F bonds. Thus, the F-P-F angles will open up to ~112° and the H-P-F angles will decrease to ~107°.
The P atom is sp3 hybridized.
The cation belongs to the C3v point group.
10. A. D. Richardson, K. Hedberg, and G. M. Lucier (p. 2787-2793) measured the structures of gas-phase WF6, ReF6, OsF6, IrF6, and PtF6. The average M-F bond distances were found to be 1.829 Å, 1.829 Å, 1.828 Å, 1.839 Å, and 1.852 Å, respectively. Are these values consistent with what you would expect based on periodic trends? Why or why not? Find the LFSE for each of these complexes. How would you expect the LFSE to affect the bond lengths? Which of these complexes would you expect to be Jahn-Teller active? For those that are Jahn-Teller active, predict the mode of distortion.
Based on the increasing Z* from W to Pt, the bond lengths should be expected to decrease from WF6 to PtF6. This prediction is not consistent with the observation.
F– is a weak ligand, so all the complexes will be high spin in an octahedral environment.
CompoundBond Length (Å)Electron Configuration LFSEJahn-Teller Active?Distortion
WF61.829W6+, d0 0 Dqt2g0eg0, No
ReF61.829Re6+, d1 4Dqt2g1eg0, Yes axial compression
OsF61.828Os6+, d2 8Dqt2g2eg0, Yes axial elongation
IrF61.839Ir6+, d3 12Dqt2g3eg0, No
PtF61.852Pt6+, d4 6Dqt2g3eg1, Yes either
With increasing LFSE, it might be expected that the bond lengths would decrease from WF6 to IrF6 and then become longer for PtF6. This is not consistent with observation, either.
The best simple explanation is to use MO theory, where the t2g orbitals are mostly nonbonding and the eg orbitals are antibonding. Then, from WF6 to IrF6 there should be little change in the M-F bond length (pretty much as observed) and then a significant increase in the Pt-F since the antibonding eg orbital becomes occupied.