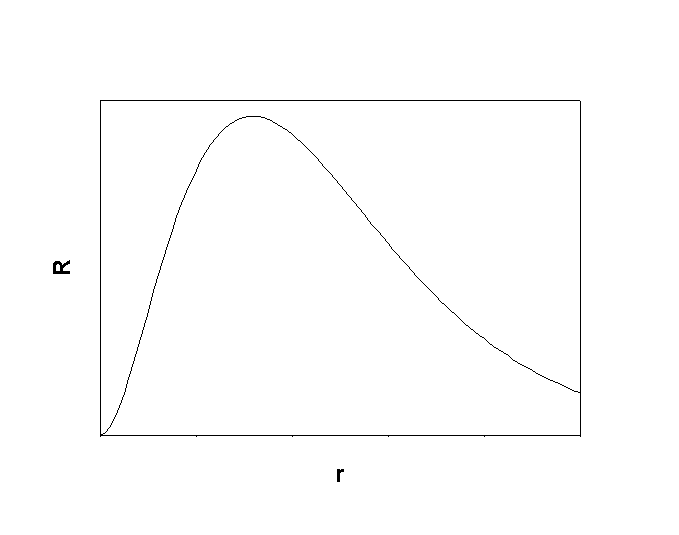
1. Give the n, l, and all of the ml quantum numbers for the 4f orbital. Sketch the radial wave function as a function of distance from the nucleus. How many radial and angular nodes are found for this orbital?
For 4f, n = 4, l = 3, ml = 3, 2, 1, 0, –1, –2, –3
0 radial nodes, 3 angular nodes.
Sketch:
2. Find the electron configuration and ground state term symbol for a) Fe; b) Mn2+; c) F–; d) V3+; e) V4+
Atom/IonElectron ConfigurationTerm Symbol
Fe[Ar]4s23d6L = 2, S = 2; so 5D
Mn2+[Ar]3d5L = 0, S = 5/2; so 6S
F–[Ne]L = 0, S = 0; so 1S
V3+[Ar]3d2L = 3, S = 1; so 3F
V4+[Ar]3d1L = 2, S = 1/2; so 2D
3. Predict the trend in the density of the first row transition metals, Sc to Zn.
Moving across the right of the Periodic Table increases atomic mass and decreases atomic radius. Density is proportional to mass/r3 so the density should increase from Sc to Zn. The observations match this prediction except for Zn (see the respective elements in the Periodic Table).
4. Write out the Born-Haber cycle required to calculate the lattice energy for MgO. Do not calculate the lattice energy, but label all of the required thermodynamic quantities.
Mg(s) + ½ O2(g) → MgO(s) ΔHfo, standard heat of formation
Mg(s) → Mg(g) S, sublimation energy
Mg(g) → Mg+(g) + e– IP1, first ionization potential
Mg+(g) → Mg2+(g) + e– IP2, second ionization potential
½ O2(g) → O(g) ½ D, bond dissociation energy
O(g) + e– → O–(g) EA1, first electron affinity
O–(g) + e– → O2–(g) EA2, second electron affinity
Mg2+(g) + O2–(g) → MgO(s) Elat, lattice energy
–ΔHfo + S + IP1 + IP2 + ½ D – EA1 – EA2 – Elat = 0
or
Elat = –ΔHfo+ S + IP1 + IP2 + ½ D – EA1 – EA2
5. Write the Lewis dot structure showing the formal charges, predict the structure including an estimate of all bond angles, and indicate the likely hybrid orbital on the central atom for the following: a) NH3; b) SF6; c) XeF2; d) XeF4.
MoleculeLewis StructureFormal Charges Geometric Structure/Bond AnglesHybrid
NH3
N = 0, H = 0 pyramidal, H-N-H ~ 107°sp3
SF6
S = 0, F = 0 octahedral, F-S-F = 90°d2sp3
XeF2
Xe = 0, F = 0 linear, F-Xe-F = 180°dsp3
XeF4
Xe = 0, F = 0 square planar, F-Xe-F = 90°sp3
