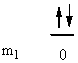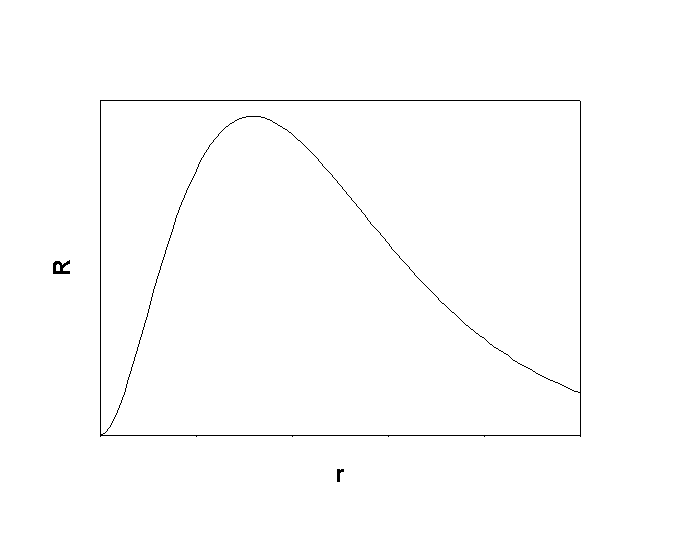
1. Give the n, l, and all of the ml quantum numbers for the first allowed g orbital. Sketch the radial wave function as a function of distance from the nucleus. How many radial and angular nodes are found for this orbital?
The first allowed g orbital is 5g, so n = 5, l = 4, and ml = 4, 3, 2, 1, 0, –1, –2, –3, –4. The number of angular nodes = l = 4, the total number of nodes is n-1 = 4, so there are 0 radial nodes. Sketch:
2. Find the electron configuration and ground state term symbol for a) Co; b) Co2+; c) Cl; d) Cl–; e) La; f) Cu; g) Cr.
a) Co[Ar]4s23d7
L = 3, S = 3/2; 4F
b) Co2+[Ar]3d7
c) Cl[Ne]3s23p5
L = 1, S = ½; 2P
d) Cl–[Ar] closed shellL = 0, S = 0; 1S
e) La[Xe]6s25d1
L = 2, S = ½; 2D
f) Cu[Ar]4s13d10
L = 1, S = ½; 2S
g) Cr[Ar]4s13d5
L = 0, S = 3; 7S
3. A periodic property not discussed in class is the absolute hardness, η, defined as η = (IP-EA)/2. Calculate η (in units of eV) for the elements Li to F. What is the general trend across this row of elements? How does the trend in η compare to the trend in Z*?
ElementIP (eV)EA (eV) η (eV)Z*
Li5.320.618 2.351.28
Be9.320 4.661.91
B8.300.277 4.012.42
C11.261.263 5.003.14
N14.53–0.07 7.303.83
O13.621.461 6.084.45
F17.423.399 7.015.01
The absolute hardness generally follows Z* but Be and N are anomalously high due the filled (Be) and half-filled (N) subshells.
4. In fluorite, CaF2, the calcium ions form the lattice and the fluoride ions occupy tetrahedral holes. Why is this unusual? Would you expect this to be a closest packed lattice, in the sense that the calcium ions are "touching"? Why or why not?
It is unusual for a cation to form the lattice but fluoride is a small anion (radius = 1.31 Å for coordination number 4). As the lattice-forming ion, calcium might be considered to have a coordination number of 12 and a radius of 1.35 Å, slightly larger than fluoride. As such, the tetrahedral holes in a closest packed lattice are much smaller than the fluoride ion so the lattice must expand to accommodate the anion. This means that the cations are not "touching".
5. The experimental lattice energies are 912 kJ/mol for AgCl and 750 kJ/mol for NaCl. The two solids have identical structures (both are rock salt) and the cationic radii for Ag+ and Na+ are identical, 0.102 nm for octahedral holes. Explain why the lattice energies are so different despite the fact the two compounds have identical structures.
Z* for Ag+ is much higher than Z* for Na+ because of the poor shielding of the d electrons. This leads to more electrostatic attraction between the anion and the cation in AgCl and a larger lattice energy. The simple models developed do not adequately account for this.
