1. Estimate the lattice energy for NaTs using both the Born-Landé and Born-Mayer equations. Assume that this hypothetical compound crystallizes in the rock salt structure. To find the anionic radius, extrapolate from the appropriate radii of the other halogens. For the Born exponent, extrapolate from the data shown below. Then average the value for the two ions. Cite the references you use to find the data you need to answer the questions. Compare the results using the two equations: do they agree? If not, what may be the sources of the differences?
Ion Electron Configurationn
[He]5
[Ne]7
[Ar]9
[Kr]10
[Xe]12
For both equations:
NA = 6.022×1023
Madelung constant A = 1.748 (Shriver, Weller, Overton, Rourke, & Armstrong, Inorganic Chemistry, 6th edition)
Z+ = +1
Z– = –1
e = 1.602×10–19 C
4πεo = 1.113×10–10 J–1C2m–1
cationic radius = r+ = 102 pm (Shriver, Weller, Overton, Rourke, & Armstrong, Inorganic Chemistry, 6th edition)
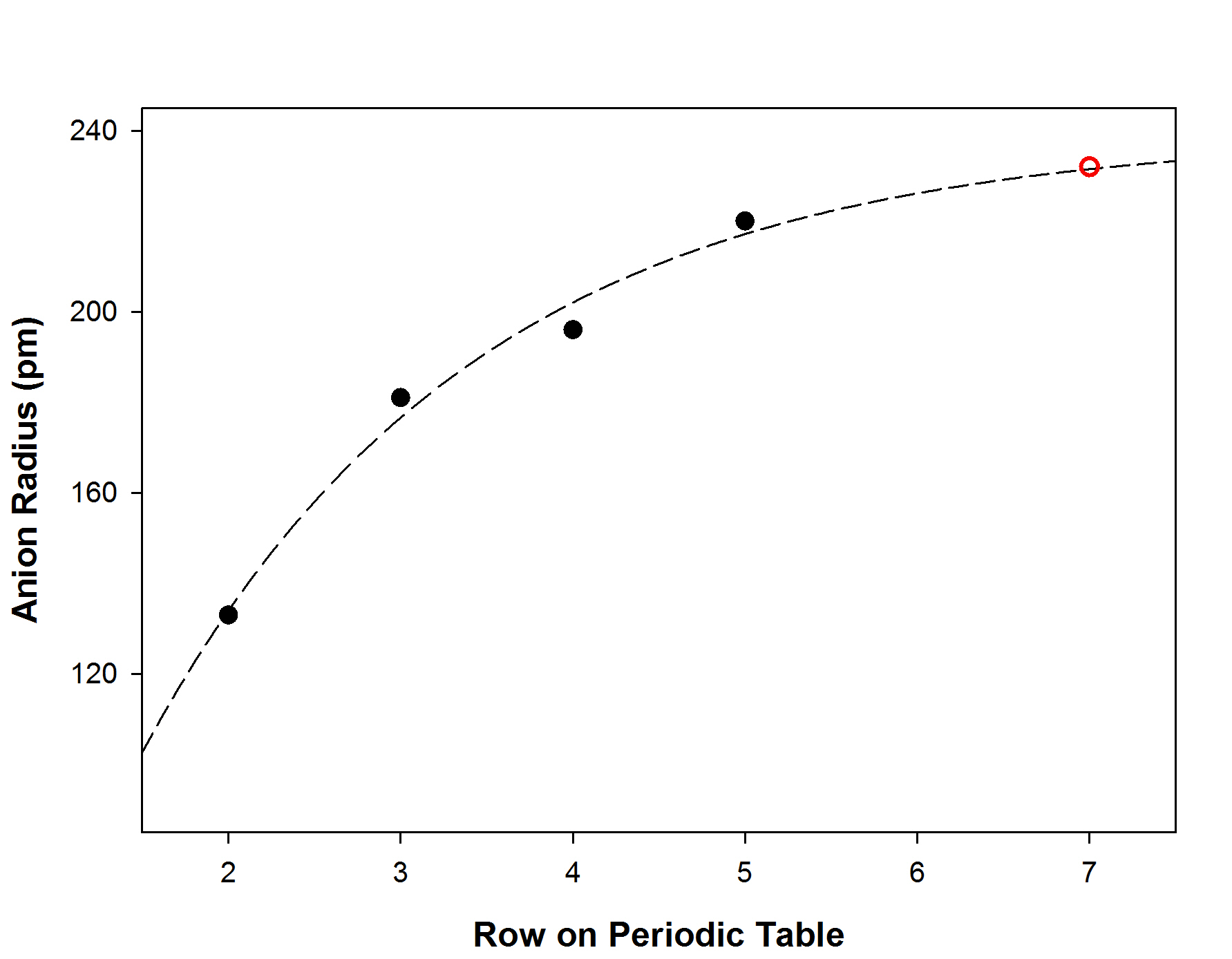
The anionic radius is found from the extrapolation of the anionic radius for the 6-coordinate halides: (Shriver, Weller, Overton, Rourke, & Armstrong, Inorganic Chemistry, 6th edition)
which gives an anionic radius (6-coordinate)) for Ts–, r– = 232 pm (red circle on the graph)
This give do = 102 + 232 = 334 pm
For the Born-Mayer equation, d* = 0.345 pm
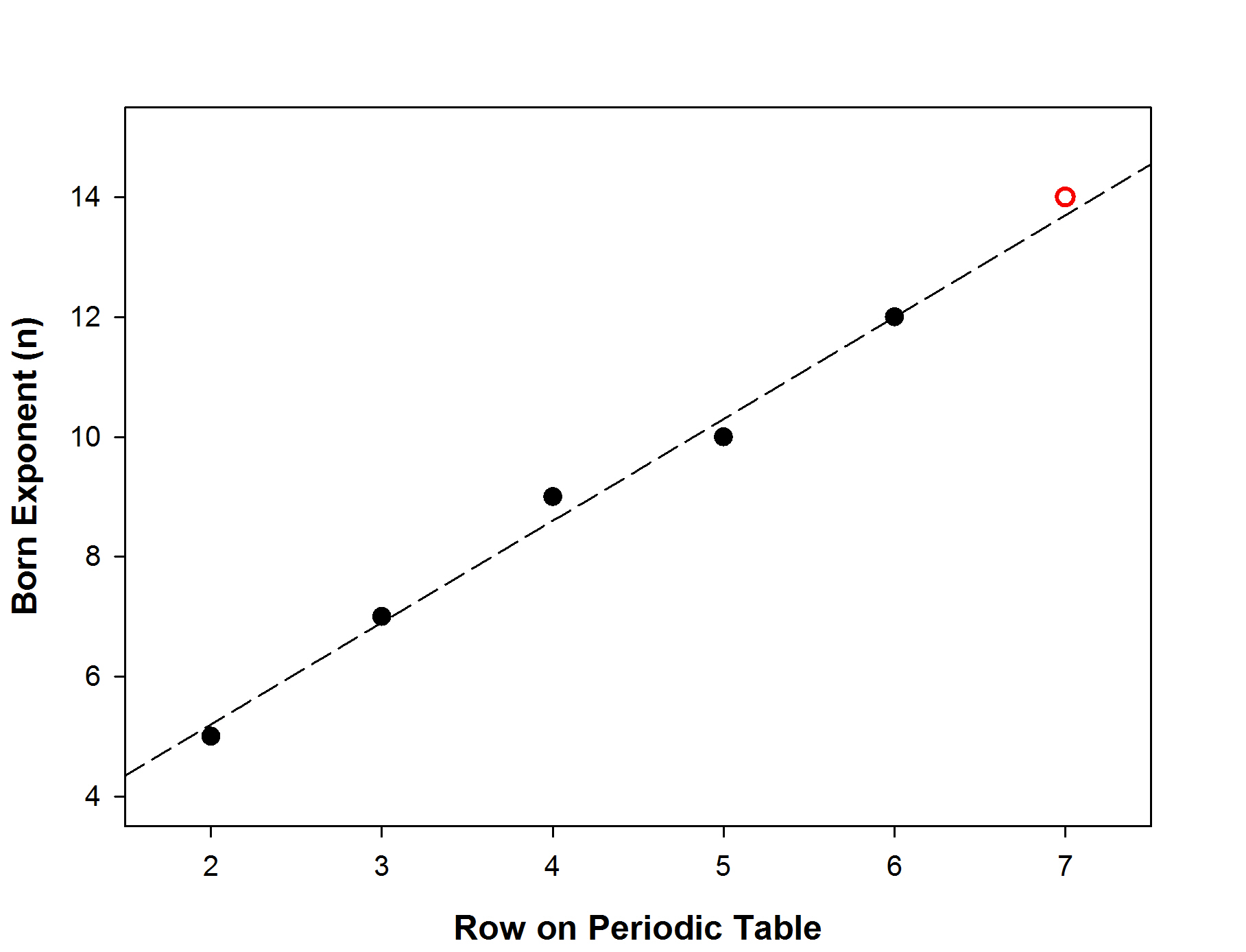
For the Born-Landé equation, the Born exponent is found by extrapolation:
which gives n = 14 (red circle on the graph)
Then n for NaTS = ½(7 + 14) = 10.5 (averaging the values for Na+, [Ne] configuration, and Ts–, [Og] configuration)
Born-Mayer: –Elat = (6.022×1023)(1.748)(+1)(–1)(1.602×10–19)2(1 – 0.345/334)/ (1.113×10–10)(3.34×10–10) = –726000 J/mol so Elat = 726 kJ/mole
Born-Landé: –Elat = (6.022×1023)(1.748)(+1)(–1)(1.602×10–19)2(1 – 1/10.5)/ (1.113×10–10)(3.34×10–10) = –796000 J/mol so Elat = 796 kJ/mole
The two values differ by less than 10 %. Given the approximations required, the two methods are in reasonable agreement.
2. Iron(II) oxide generally is found as a nonstoichiometric compound, Fe1–δO, where δ is small (< 0.1). Is nonstoichiometric FeO an n-type or p-type semiconductor? Explain your reasoning. Hint: remember charge balance.
Using the hint, the charge balance is achieved by some of the Fe2+ being oxidized to Fe3+. Suppose that the stoichiometry of the Fe2+ is x and the stoichiometry of the Fe3+ is y. Then, x + y = 1 – δ (stoichiometry) and 2x + 3y = 2 (charge balance). Solving the two equations gives x = 1 – 3δ and y = 2δ, or the compound stoichiometry can be written as (Fe2+)1 – 3δ(Fe3+)2δO. Since there is an excess of positive charge, this must be a p-type semiconductor.
