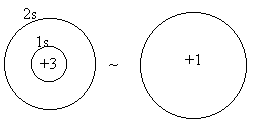Chemistry 401

Multielectron atoms

We can not solve the Schroedinger equation exactly so assumptions must be made.

Usual assumption: the hydrogenic obitals are adequate and electrons occupy them in some fashion.

 

The occupation of electrons in orbitals is called the electron configuration – this is one way to describe the electronic properties of atoms.

 

Two guiding principals used to account for electron configurations:

Aufbau Principle: electrons occupy orbitals in such a manner to give the lowest possible total energy

Pauli Exclusion Principle: each electron in an atom is described by a unique set of quantum numbers (n, l, m_l, m_s) - i.e., two electrons per hydrogenic orbital

Periodic Table: based on electron configurations and can be used to predict them but not absolute (electron configurations are experimental quantities)

Aids in finding correct electron configurations from the Periodic Table:

Half-filled phenomenon: when d or f electrons are the valence shell, if a shift of 1 electron (occasionally 2 but this is not predictive) from an s orbital to the d or f orbital leads to a filled or half filled d or f orbital, this will stabilize the electron configuration.

Anions: add electrons to the neutral atom and follow above rules.

Cations: electrons are always removed from the orbitals of neutral atoms with the largest principal quantum number (n); the remaining electrons fill the orbitals with the lowest n consistent with the Pauli Principle

 

Term Symbols

Another way to indicate electron configurations

A term symbol gives the required information about the angular momentum quantum numbers l, m_<l, and m_s

For Ground States of atoms:

1) Only consider unfilled subshells; filled shells do not contribute

2) Fill the valence electrons into the unfilled subshell such that the highest total spin is attained using the highest possible m_l values (this is Hund's Rule)

3) L = Σm_l

4) S = Σm_s

5) The term symbol is written as ^2S+1L

2S+1 is called the total spin multiplicity or degeneracy and is written as a number

L is the total orbital angular momentum and is written as a letter:

Lletter designation

 

0S

 

1P

 

2D

 

3F

 

4G

 

5H

 

6I

 

Periodic Properties

 

Consider Li:

How good is such an approximation?

pretty good for s orbitals - they overlap the nucleus

mediocre for p orbitals - nodal at the nucleus

poor for d or f orbitals - multiply nodal at the nucleus

The reduction of nuclear charge seen by outer electrons due to the inner electrons is called screening or shielding

quantitatively:

Z* = Z - σ

Z* = effective nuclear charge

Z = true nuclear charge

σ = shielding constant

Shielding constants are established by ad hoc rules or quantum mechanical calculations

Trends in Z*

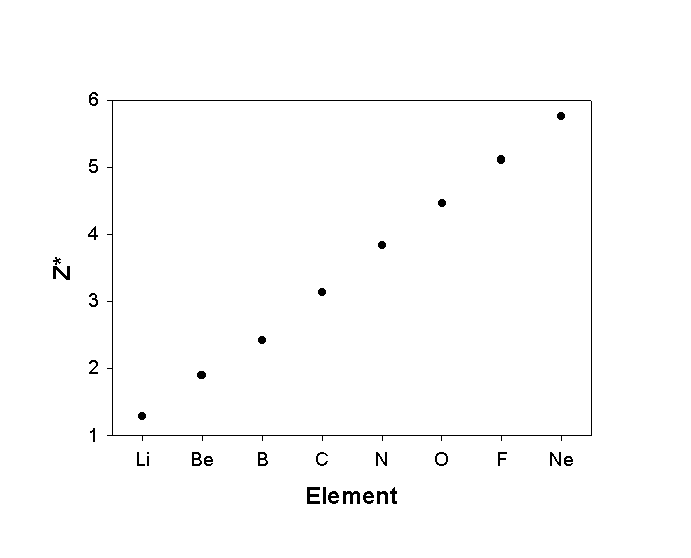
s orbitals are good screeners, p orbitals are moderate screeners; d, f orbitals are very poor screeners.

This means changes across the Table are bigger than changes down the Table

 

Experimental Properties

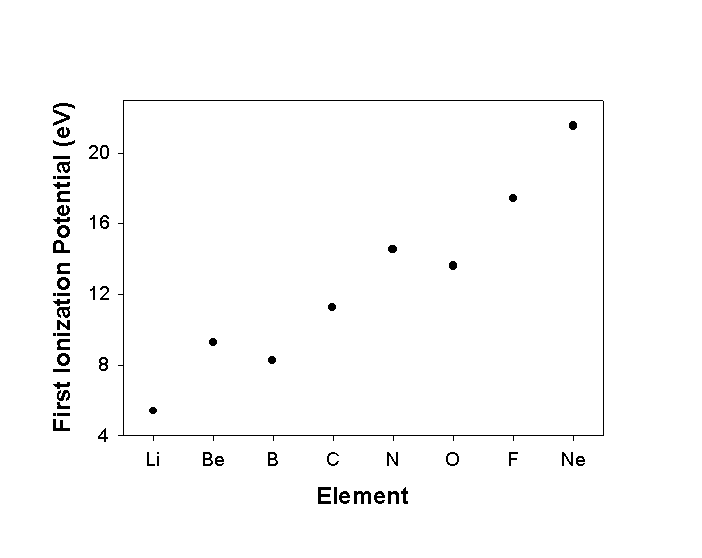
Ionization Potential (IP) or Ionization Energy (IE)

A(g) A⁺(g) + e^–

The energy associated with this reaction is the ionization energy

IP or IE is thermodynamically positive

IP generally follows Z* across the Table

 

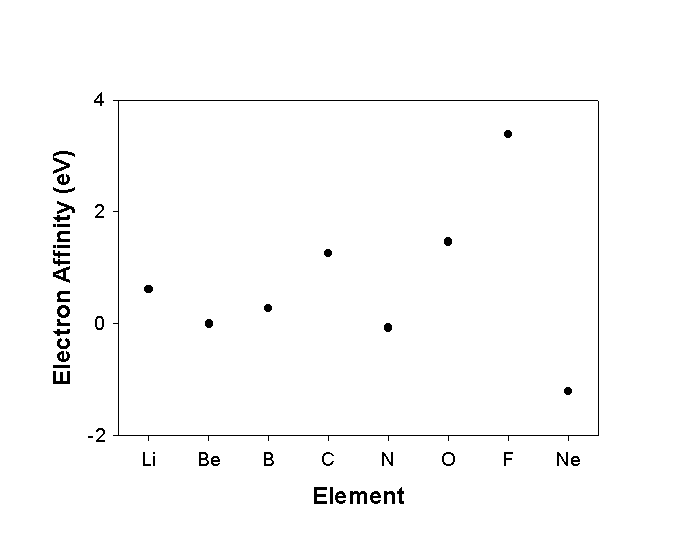
Electron Affinity : EA

A(g) + e^–A^–(g)

EA reported with the wrong thermodynamic sign

Periodic trends are reverse of IP

Atomic Size : Radius of an atom - a difficult concept to define

atomic radius depends upon the bonding situation

metallic radius : ½ the internuclear distance between atoms in the metallic state

covalent radius : ½ the internuclear distance in a homonuclear covalent bond

ionic radius : size of an ion in a solid

van der Waals radius : the distance at which an atom just starts to respond to interactions from neighboring atoms

radii all of different numerical values but similar periodic trends:

r increases as go down the Periodic Table (bigger n)

r decreases as go across the Periodic Table (bigger Z*)