 Final Exam, Spring 1999
Final Exam, Spring 1999 Final Exam, Spring 1999
Final Exam, Spring 19991. Complete and balance the following reactions.
a. HCl(aq) + NaOH(aq)
b. NiCl2(aq) + NaOH(aq)
c. (CH3)3N(aq) + H2O(l)
d. Zn2+(aq) + H2O(l)
e. Zn2+(aq) + NH3(aq)
f. Ca(OH)2(s) + H2SO4(aq)
g. HCl(aq) + HCO3-(aq)
h. Co(NO3)2(aq) + H2S(aq)
i. Cr2O72-(aq) + NO(g) → Cr3+(aq) + HNO3(aq)
j. H2O2(aq) + Fe(s) → Fe(OH)2(s)
a. HCl(aq) + NaOH(aq) → H2O(l) + Na+(aq) + Cl–(aq)
b. NiCl2(aq) + 2 NaOH(aq) → Ni(OH)2(s) + 2 Na+(aq) + 2 Cl–(aq)
c. (CH3)3N(aq) + H2O(l) → ← (CH3)3NH+(aq) + OH–(aq)
d. Zn2+(aq) + 2 H2O(l) → ← ZnOH+(aq) + H3O+(aq)
e. Zn2+(aq) + 4 NH3(aq) → ← [Zn(NH3)4]2+(aq)
f. Ca(OH)2(s) + H2SO4(aq) → CaSO4(s) + 2 H2O(l)
g. HCl(aq) + HCO3–(aq) → H2CO3(aq) + Cl–(aq)
h. Co(NO3)2(aq) + H2S(aq) + 2 H2O(l) → CoS(s) + 2 H3O+(aq) + 2 NO3–(aq)
i. Cr2O72–(aq) + NO(g) → Cr3+(aq) + HNO3(aq)
Oxidation: NO(g) + 2 H2O(l) → HNO3(aq) + 3 H+(aq) + 3 e–
Reduction: Cr2O72–(aq) + 14 H+(aq) + 6 e– → 2 Cr3+(aq) + 7 H2O(l)
Net: Cr2O72–(aq) + 2 NO(g) + 8 H+(aq) → 2 Cr3+(aq) + 2 HNO3(aq) + 3 H2O(l)
j. H2O2(aq) + Fe(s) → Fe(OH)2(s)
Balanced as shown.
2. Methane, CH4, is the primary component of natural gas and is a clean burning, high energy density fuel:
CH4(g) + O2(g) → CO2(g) + H2O(g)
a. Find ΔH° for the combustion of methane.
b. Find ΔS° for the combustion of methane.
c. Find ΔG° for the combustion of methane at 25 °C.
d. Estimate ΔG° for the combustion of methane at 400 °C
e. Estimate the maximum amount of work possible for the combustion of 1.00 mol of methane at 400 °C.
Balance the reaction: CH4(g) + 2 O2(g) → CO2(g) + 2 H2O(g)
a. ΔH° = [(–393.5) + 2(–241.8)] – [(–74.81) + 2(0)] = –802.3 kJ/mol
b. ΔS° = [(213.6) + 2(188.7)] – [(186.2) + 2(205.0)] = –5.2 J/mol·K
c. ΔG° –802.3 – (298)(–0.0052) = –800.8 kJ/mol
d. ΔG° –802.3 – (673)(–0.0052) = –798.8 kJ/mol
e. wmax = ΔG° = –798.8 kJ
3. The following rate data was determined for the decomposition of nitrogen dioxide into nitrogen and oxygen.
T (°C)k (L/mol·s)
3200.514
3300.789
3401.006
3501.710
a. Write the balanced reaction.
b. Make an Arrhenius plot of the data.
c. From your plotted data, estimate the activation energy for the reaction.
d. What is the order of the reaction?
a. 2 NO2(g) → N2(g) + 2 O2(g)
b. 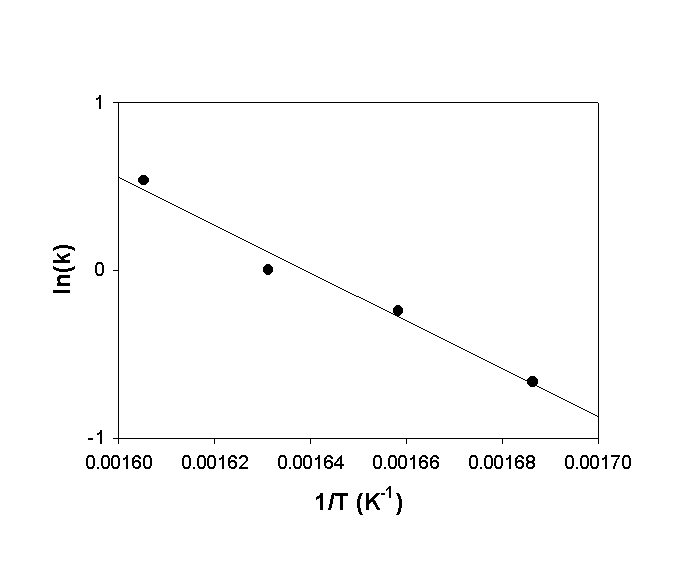
c. Slope = –14000, so Ea = –slope×R = –(–14000)×8.314 = 120000 J/mol = 120 kJ/mol
d. The units of the rate constant indicate that the order of the rate law = 2.
4. Find the value of Ka for the hydronium ion.
The reaction is defined by the definition of Ka, where the weak acid is hydronium ion. Thus:
H3O+(aq) + H2O(l) → ← H3O+(aq) + H2O(l)
The mass action expression then is Ka = [H3O+]e/[H3O+]e = 1
Another way to approach this is for a reaction in which products and reactant are the same, ΔG° = 0, so 0 = –RTln Ka, which gives Ka = e–0/RT = 1
5. A 0.0010 M solution of (CH3)2NH is prepared at 25 °C.
a. What is the pH of the solution?
b. 50.0 mL of the dimethylamine solution is mixed with 1.0 mL of 0.025 M HCl. What is the pH of the mixed solution at 25 °C?
a. To find the pH of the initial solution, use the standard approach to equilibrium problems:
(CH3)2NH(aq) + H2O(l) → ← (CH3)2NH2+(aq) + OH–(aq)
Kb = [(CH3)2NH2+]e [OH–]e/[(CH3)2NH]e = 1.0×10–14/1.7×10–11 = 5.9×10–4
Initial0.001000
Change–x+x+x
Equilibrium0.0010 – xxx
Approximate? 0.0010/5.9×10–4 = 1.7 < 100 No
5.9×10–4 = x2/(0.0010 – x)
x2 + 5.9×10–4x – 5.9×10–7 = 0
x = 5.3×10–4 or –1.1×10–3
pOH = –log5.3×10–4 = 3.28
pH = 14.00 – 3.28 = 10.72
b. Creating the buffer:
CH3)2NH(aq) + HCl(aq) → (CH3)2NH2+(aq) + Cl–(aq)
(CH3)2NH(aq) + H2O(l) → ← (CH3)2NH2+(aq) + OH–(aq)
Kb = [(CH3)2NH2+]e [OH–]e/[(CH3)2NH]e = 1.0×10–14/1.7×10–11 = 5.9×10–4
Initial0.001000
A/B–(0.025×1.0)/51.0(0.025×1.0)/51.0
Change–x+x+x
Equilibrium(0.0010×50.0 – (0.025×1.0) – x)51.0 ((0.025×1.0) + x)/51.0x
5.9×10–4 = [x(0.025 + x)/51.0]/[(0.025 – x)/51.0] = x(0.025 + x)/(0.025 – x)
x2 + 0.02441x – 1.475×10–5 = 0
x = 5.9×10–4 or –2.5×10–2
pOH = –log5.9×10–4 = 3.23
pH = 14.00 – 3.23 = 10.72
The number of moles of base and conjugate acid are the same so that pH = pKa. Adding acid should have caused the pH to drop a little bit but the dilution of the solution countered this so that the pH for the two solutions is unchanged.
6. This question is concerned with the chemistry of carbon dioxide. Consider the reaction of carbon dioxide with water at 25 °C:
CO2(g) + H2O(l) → ← H2CO3(aq)
a. Find ΔH°.
b. Find ΔS°.
c. Find ΔG° at 25 °C.
d. Find the thermodynamic equilibrium constant for the reaction at 25 °C.
e. The atmospheric pressure of carbon dioxide is 0.00036 atm. Find the concentration of carbonic acid under these conditions.
f. Find the pH of an aqueous solution in equilibrium with atmospheric carbon dioxide.
a. ΔH° = [–698.7] – [(–395.5) + (–285.8)] = –17.4 kJ/mol
b. ΔS° = [191] – [(213.6) + (69.91)] = –93 J/mol·K
c. ΔG° = –17.4 – (298)(–0.093) = 10.3 kJ/mol
d. ΔG° = –RTln Kp so Kp = e–10300/(8.314×298) = 0.016
e. This is an equilibrium problem:
CO2(g) + H2O(l) → ← H2CO3(aq)
Kp = [H2CO3]e/PCO2e = 0.016
Initial0.000360
Change–x+x
Equilibrium0.00036 – xx
0.016 = x/(0.00036 – x)
5.76×10–6 – 0.016x = x
1.016x = 5.76×10–6
x = 5.7×10–6 = [H2CO3]
f. This is a diprotic weak acid, where the second ionization can be ignored.
H2CO3(aq) + H2O(l) → ← H3O+(aq) + HCO3–(aq)
Ka = [H3O+]e[HCO3–]e /[H2CO3]e = 4.4×10–7
Initial5.7×10–60 0
Change–x+x +x
Equilibrium5.7×10–6 – xx x
No approximation
4.4×10–7 = x2/(5.7×10–6 – x)
x2 + 4.4×10–7x – 2.508×10–12 = 0
x = 1.4×10–6 or –1.8×10–6
pH = –log(1.4×10–6) = 5.85
7. Consider CoS.
a. What is the molar solubility in pure water at 25 °C?
b. What is the molar solubility in 0.010 M Co(NO3)2 solution?
a. What is the molar solubility in pure water at 25 °C?
CoS(s) → ← Co2+(aq) + S2–(aq)
Ksp = [Co2+]e[S2–]e = 4×10–21
Initial00
Change+x+x
Equilibriumxx
4×10–21 = x2
x = 6×10–11 M = CoS solubility
b. What is the molar solubility in 0.010 M Co(NO3)2 solution?
Co(NO3)2(aq) → Co2+(aq) + 2 NO3–(aq)
CoS(s) → ← Co2+(aq) + S2–(aq)
Ksp = [Co2+]e[S2–]e = 4×10–21
Initial0.0100
Change+x+x
Equilibrium0.010 + xx
4×10–21 = x(0.010)
x = 4×10–19 M = CoS solubility in the cobalt nitrate solution
8. The commercial alkaline dry cell is Zn(s) | Zn(OH)2(s) || MnO2(s) | Mn2O3(s) | C(s) and the electrolyte for both half-cells is an aqueous paste of potassium hydroxide.
a. Write the oxidation half-reaction under the pH conditions of the cell.
b. Write the reduction half-reaction under the pH conditions of the cell.
c. Write the net reaction under the pH conditions of the cell.
d. E° for the cell is 1.5 V. Find the cell potential when the reactants are 25% consumed.
e. A cell is built using 10.0 g of each reactant. Assume that the cell dies because the limiting reagent is consumed. If you are using this battery in your portable CD player that draws 1.0 mA, how many hours can you listen to music at the beach?
a. Zn(s) + 2 OH–(aq) → Zn(OH)2(s) + 2 e–
b. 2 MnO2(s) + H2O(l) + 2 e– → Mn2O3(s) + 2 OH–(aq)
c. Zn(s) + 2 MnO2(s) + H2O(l) → Zn(OH)2(s) + Mn2O3(s)
d. Since all of the cell components are pure liquids or solids, the cell potential does not change as the componemts are consumed. Thus, E° = 1.5 V
e. 10.0 g Zn = 10.0/65.4 = 0.153 mol
10.0 g MnO2 = 10.0/(54.9 + 2(16.0)) = 0.115 mol so this is the limiting reagent.
Each mole of MnO2 requires 1 mole of electrons, so 0.115 mol of electrons will transfer.
A = 1.0 mA = 0.0010 A; F = 96485 coul/mol; n = 0.115 mol, so
t = nF/A = (0.115)(96485)/(0.0010) = 1.1×107 s
1.1×107 s/3600 s/hr = 3100 hr.