Exam 3A, Spring 1999

1. Complete and balance the following reactions:

a. HCO3–(aq) + H2O(l)

b. HPO42–(aq) + NaOH(aq)

c. Fe(NO3)2(aq) + H2O(l)

d. Mn(NO3)2(aq) + KOH(aq)

e. CaCl2(aq) + H2SO4(aq)

f. AgNO3(aq) + NaCN(aq)

Answer

a. HCO3–(aq) + H2O(l) → ← H2CO3(aq) + OH–(aq)

pKa of bicarbonate = 10.32; pKb of bicarbonate = 14.00 - 10.32 = 3.68 so it is a stronger base.

b. HPO42–(aq) + NaOH(aq) → H2O(l) + Na+(aq) + PO43–(aq)

c. Fe(NO3)2(aq) + H2O(l)

Fe(NO3)2(aq) → Fe2+(aq) + 2 NO3–(aq)

Fe2+(aq) + 2 H2O(l) → ← FeOH+(aq) + H3O+(aq)

d. Mn(NO3)2(aq) + 2 KOH(aq) → Mn(OH)2(s) + 2 K+(aq) + 2 NO3–(aq)

e. CaCl2(aq) + H2SO4(aq) + 2 H2O(l) → CaSO4(s) + 2 H3O+(aq) + 2 Cl–(aq)

f. AgNO3(aq) + 2 NaCN(aq) → ← Ag(CN)2–(aq) + 2 Na+(aq) + NO3–(aq)

2. On the titration curve shown, give estimates for the following: the pH at the equivalence point, the equivalence volume, and the pKa.

Answer

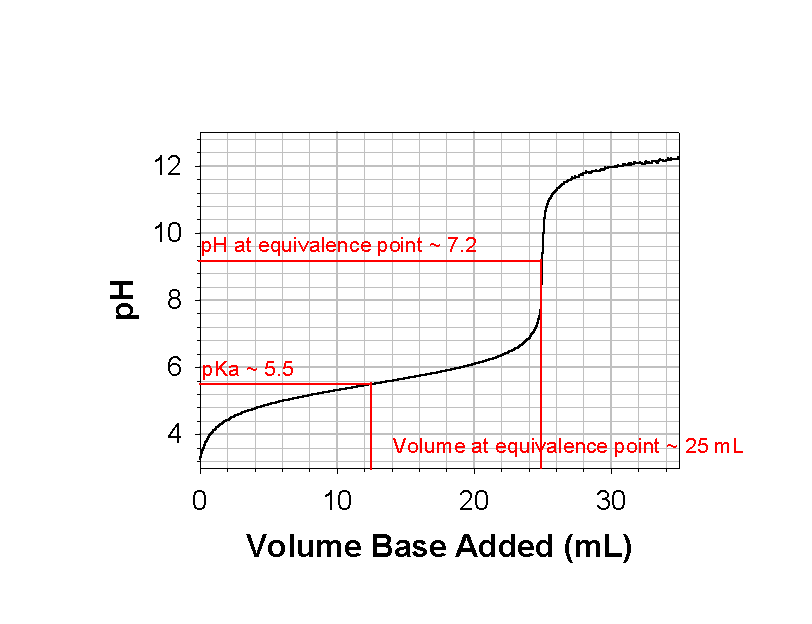
3. Consider a 0.35 M solution of aniline, C6H5NH2, at 25 °C.

a. What is the pH of the solution?

b. What is the pH of the solution if enough anilinium hydrobromide, C6H5NH3Br, is added so that the anilinium ion concentration becomes 0.35 M?

Answer

a. What is the pH of the solution?

C6H5NH2(aq) +H2O(l) → ← C6H5NH3+(aq) +OH–(aq)

Kb = [C6H5NH3+]e[OH–]e                                 [C6H5NH2]e = 10–(14.00 – pKa) = 10–(14.00 – 4.85) = 10–9.15 = 7.1×10–10

Initial0.3500

Change–x+x+x

Equil.0.35 – xxx

Approximate? 0.35/7.1×10–10 = 4.9×108 > 100 so Yes

7.1×10–10 = x2/0.35

x = [OH–]e = 1.6×10–5

pOH = –log(1.6×10–5) = 4.80

pH = 14.00 – 4.80 = 9.20

b. What is the pH of the solution if enough anilinium hydrobromide, C6H5NH3Br, is added so that the anilinium ion concentration becomes 0.35 M?

When the concentration of the base and the conjugate acid are the same, pH = pKa = 4.85

4. Consider cadmium hydroxide at 25 °C.

a. What is the molar solubility in pure water?

b. What is the molar solubility in 1.0 M Cd(NO3)2 solution?

c. What is the molar solubility in 1.0 M NH3 solution?

Answer

a. What is the molar solubility in pure water?

Cd(OH)2(s) → ← Cd2+(aq) +2 OH–(aq)

Ksp = [Cd2+]e[OH–]e2 = 2.5×10–14


Initial00

Change+x+2x

Equil.x2x

2.5×10–14 = 4x3

x = molar solubility = 1.8×10–5 M

b. What is the molar solubility in 1.0 M Cd(NO3)2 solution?

Cd(NO3)2(s) → Cd2+(aq) +2 NO3–(aq)

Cd(OH)2(s) → ← Cd2+(aq) +2 OH–(aq)

Ksp = [Cd2+]e[OH–]e2 = 2.5×10–14


Initial1.00

Change+x+2x

Equil.1.0 + x2x

1.0 + x ~ 1.0

2.5×10–14 = 4x2

x = molar solubility = 7.9×10–8 M

c. What is the molar solubility in 1.0 M NH3 solution?

Cd(OH)2(s) → ← Cd2+(aq) +2 OH–(aq)

Cd2+(aq) +4 NH3(aq) → ← Cd[NH3]42+(aq)

Net:Cd(OH)2(s) +4 NH3(aq) → ← Cd[NH3]42+(aq) + 2 OH–(aq)

Kc = [Cd[NH3]42+]e[OH–]e2                                    [NH3]e4 = Ksp×Kf = 2.5×10–14×1.3×107 = 3.3×10–7



Initial1.000

Change– 4x+x+2x

Equil.1.0 – 4xx2x

1.0 – 4x ~ 1.0

3.3×10–7 = 4x3

x = molar solubility = 4.4×10–3 M

5. You are given 1.0 M solutions of sodium dihydrogen phosphate and sodium hydrogen phosphate. How many mL of each solution are required to prepare 100.0 mL of a buffer with pH = 7.00 at 25 °C.

Answer

H2PO4–(aq) +H2O(l) → ← H3O+(aq) +HPO42–(aq)

Ka = [H3O+]e[HPO42–]e                                 [H2PO4–]e = 6.3×10–8

InitialVa×1.0/100.00 (100.0 –Va)×1.0/100.0

Change–x+x+x

Equil.Va×1.0/100.0 – xx (100.0 –Va)×1.0/100.0 + x



Approximate 1.0/6.3×10–8 = 1.6×107 > 100 so Yes

x = [H3O+]e = 10–pH = 10–7.00 = 1.0×10–7

6.3×10–8 = (1.0×10–7)((100.0 – Va)×1.0/100.0)/(Va×1.0/100.0)

6.3×10–1 = (100.0 – Va)/Va

1.63Va = 100.0

Va = 61 mL = volume of sodium dihydrogenphosphate solution required.

100 – 61 = 39 mL = volume of sodium hydrogenphosphate solution require.