 Exam 1B, Spring 2005
Exam 1B, Spring 2005 Exam 1B, Spring 2005
Exam 1B, Spring 20051. Nomenclature:
a. Give the name for Cr2O72–
b. Give the molecular formula for the dihydrogen phosphate ion.
a. dichromate ion
b. H2PO4–
2. Briefly (15 words or less) distinguish between an activated complex and an intermediate.
Intermediate: molecule temporarily formed by a collision in a reaction. Activated complex: highest energy intermediate.
3. For the reaction shown below:
CO(g) + NO(g) → CO2(g) + N2(g)
a. What is the ratio of the rate of loss of nitrogen oxide compared to the rate of gain of nitrogen?
b. Is this an elementary reaction? Why or why not?
2 CO(g) + 2 NO(g) → 2 CO2(g) + N2(g)
Since the stoichiometric ration between nitrogen oxide and nitrogen is 2, the rate of loss of nitrogen oxide is twice the rate of gain of nitrogen.
b. Since there is no mechanistic information given, one can not determine absolutely. However, since the reaction requires a 4-particle collision, it is unlikely that this is an elementary reaction.
4. Consider the following reaction:
H2O2(aq) → H2O(l) + O2(g)
which has a rate law of Rate = –k, where k = 1.0×10–3 M s–1. If [H2O2]initial = 1.0 M and [O2]initial = 0.0 M, answer the following questions:
a. What is the order of reaction with respect to hydrogen peroxide?
b. What is the concentration of hydrogen peroxide at t = 100 s?
c. What is the concentration of oxygen at t = 100 s?
a. The rate law given is zero order. Since there is only one reacting component, hydrogen peroxide, the order with respect to hydrogen peroxide must be zero.
b. Use the definition of rate, the rate law, and the initial concentration of hydrogen peroxide:
Rate = –1.0×10–3 M s–1 = Δ[H2O2]/Δt
–1.0×10–3 M s–1 = ([H2O2]final – 1.0 M)/100 s
[H2O2]final = 0.9 M
c. From the amount of hydrogen peroxide consumed, 0.1 M, and the stoichiometric ratio between hydrogen peroxide and oxygen, 2, the amount of oxygen formed must be 0.05 M
5. The data listed below was collected for the following reaction:
2 HgCl2(aq) + C2O42–(aq) → 2 Cl–(aq) + 2 CO2(g) + Hg2Cl2(s)
Experiment [HgCl2] (M) [C2O42–] (M) Initial Rate (M min–1)
1 0.10 0.20 4.0×10–5
2 0.10 0.40 1.6×10–4
3 0.050 0.40 8.0×10–5
4 0.050 0.20 2.0×10–5
a. What is the rate law for the reaction?
b. What is the value of the rate constant for the reaction?
a. Use the Method of Initial Rates to find the orders of reaction:
To find the order in mercury(II) chloride, use either experiments 1 & 4 or experiments 2 & 3. In either case, doubling the mercury(II) chloride concentration doubles the initial rate, which means that the reaction is first order in mercury(II) chloride. To find the order in oxalate ion, use either experiments 1 & 2 or experiments 3 & 4. In either case, doubling the oxalate ion concentration quadruples the initial rate, which means that the reaction is second order in oxalate ion. Thus, the rate law is:
Rate = –k[HgCl2][C2O42–]2
b. To find the rate constant, use the (now established) rate law and one of the experimental concentrations and then solve for k. Using experiment 1 data:
k = 4.0×10–5/[0.10][0.20]2
k = 1.0×10–2 M–2 min–1
Any choice of experiments gives the same value for k.
6. The following mechanism was proposed for a reaction:
OCl–(aq) + H2O(l)→ ← HOCl(aq) + OH–(aq)
I–(aq) + HOCl(aq) → HOI(aq) + Cl–(aq)
HOI(aq) + OH–(aq) → H2O(l) + OI–(aq)
a. Write the net reaction.
b. What is the molecularity of each reaction in the mechanism?
c.Which step is not rate determining? Why?
a. Add all the reactions together and eliminate common species to give:
OCl–(aq) + I–(aq) → OI–(aq) + Cl–(aq)
b. All reactions are bimolecular.
c. The first step is almost certainly not rate-determining because it involves reaction with the solvent, water, which is in much higher concentration than any other species in solution.
7. Write the mass action expression for Kc for the following reactions.
a. CO2(g) + H2(g) → ← CO(g) + H2O(g)
b. NO(g) + H2O(g) → ← O2(g) + NH3(g)
c. NH4HS(s) → ← H2S(g) + NH3(g)
a. Fortunately, the reaction is already balanced, so:
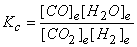
b. First, balance the reaction:
4 NO(g) + 6 H2O(g) → ← 5 O2(g) + 4 NH3(g)
Then:
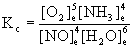
c. The reaction is already balanced, so:
Kc = [H2S]e[NH3]e
8. For the reaction:
N2(g) + O2(g) → ← 2 NO(g)
Kc = 4×10–4.
Find Kc for the reaction:
NO(g) → ← ½ N2(g) + ½ O2(g)
First, reverse the given reaction:
2 NO(g) → ← N2(g) + O2(g)
This causes Kc to be inverted: Kc(new) = 1/Kc(given) = 1/(4×10–4) = 1/4 ×104
To get to the desired reaction, all stoichiometric coefficients are halved. This means the square root of Kc(new) must be taken:
Kc(final) = (Kc(new))½ = (1/4 ×104)½ = 1/2 ×102 = 50