 Exam 1B, Spring 2004
Exam 1B, Spring 2004 Exam 1B, Spring 2004
Exam 1B, Spring 20041. Nomenclature:
a. Give the name for H2PO4–
b. Give the molecular formula for the nitrite ion.
a. dihydrogen phosphate ion
b. NO2–
2. The following reaction has a rate constant k = 1.0×10–10 s–1 at 25 °C.
[Co(NH3)6]2+(aq) + H2O(l) → [Co(NH3)5(H2O)]2+(aq) + NH3(aq)
a. Write the rate law for the reaction.
b. What is the initial rate of reaction if the initial concentration of [Co(NH3)6]2+ is 1.0 M?
c. If the initial concentration of [Co(NH3)6]2+ is 1.0 mM, what is the half-life of the reaction?
d. Is this an elementary reaction? Why or why not?
a. The units of the rate constant indicate that this is a first order reaction. Since the water is indicated as a pure liquid, i.e., the solvent, the reaction rate must be controlled by the other reactant. Thus, the rate law must be:
Rate = –k[ [Co(NH3)6]2+ ]
b. Rate = –k[ [Co(NH3)6]2+ ]
Rate = (1.0×10–10 s–1)(1.0 M)
Rate = 1.0×10–10 M s–1 of loss of reactants.
c. Since this is a first order reaction, the half-life is independent of the initial concentration. Therefore:
t½ = 0.693/(1.0×10–10 s–1) = 6.9×10+9 s
d. There is no way to tell if this is an elementary reaction since no information about the mechanism is given.
3. A student measured the rate constants at several temperatures for the following reaction and made the plots shown.
[Ir(Cl)(CO)(P(C6H5)3)2](benzene) + H2(g) → [Ir(H2)(Cl)(CO)(P(C6H5)3)2](benzene)
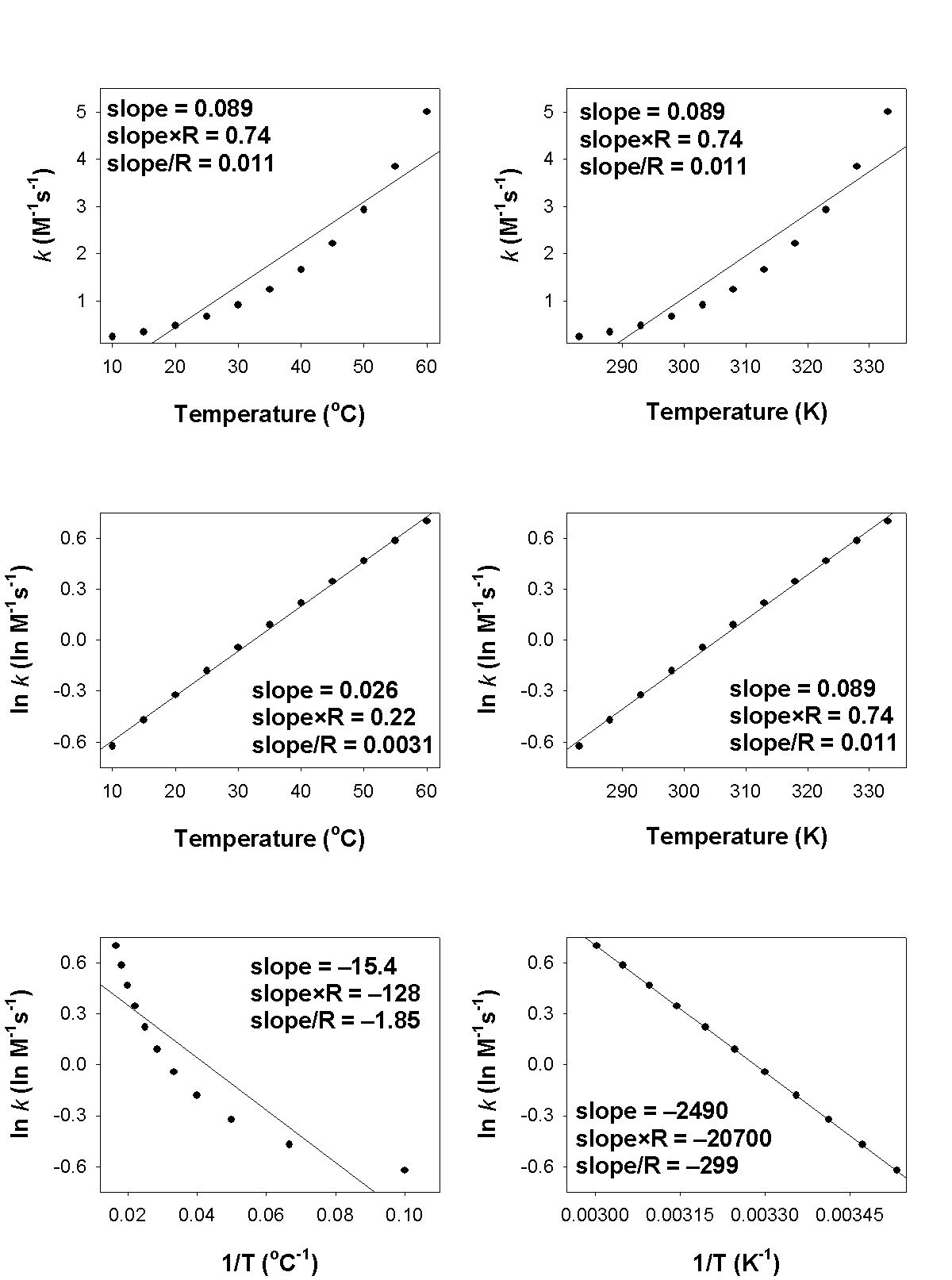
a. What is the order of reaction?
b. What is the rate constant for the reaction at 50 °C?
c. What is the activation energy in units of kJ/mol? The value of R used for the indicated calculations is 8.314 J/mol•K
a. The units of the rate constant indicate that the order of reaction is 2.
b. The plot of k vs. T (°C) allows estimation of the rate constant: at T = 50 °C is about 3 M–1s–1
c. Activation energies are found from a plot of ln k vs. 1/T (T in K). Ea = –slope×R = –(–20700) = 20700 J/mol·K = 20.7 kJ/mol·K
4. The data listed below was collected for the following reaction:
[Cr(CO)4(P(OC6H5)3)(As(C6H5)3)] → products
Time (min)Concentration (M)
20.374
70.312
140.259
220.203
320.155
430.108
540.078
670.050
a. What is the order of reaction?
b. Estimate the half-life in units of minutes.
a. In the first portion of the reaction, the concentration of the reactant changes from 0.374 M to half this value (0.187 M) between 20 and 30 minutes, so the half-life is approximately 25 minutes. Likewise, in the latter portion of the reaction the concentration approximately halves from 0.108 M to 0.050 M in 24 minutes (67 min – 43 min = 24 min). Since the half-life is independent of the concentration of reactant, this means the reaction must be first order.
A similar conclusion could be found by using the method of initial rates over two different time intervals during the reaction. For example, the rate for the first two data points is Rate = [0.312 – 0.374]/[7 – 2] = –0.062/5 = –0.01 M/min. Using the fourth and fifth data points gives Rate = [0.155 – 0.203]/[32 – 22] = –0.048/10 = –0.0048 M/min. Since the rate approximately doubles when the concentration is about doubled, the order of reaction must be 1.
b. Using the reasoning given above, the half-life must be about 24 min.
5. The following mechanism was proposed for a reaction:
[IrCl6]2–(aq) + [W(CN)8]4–(aq) → ← [IrCl62–---W(CN)84– ](aq)
[IrCl62–---W(CN)84– ](aq) → ← [IrCl63–---W(CN)83– ](aq)
[IrCl63–---W(CN)83– ](aq) → ← [IrCl6]3–(aq) + [W(CN)8]3–(aq)
a. Write the net reaction.
b. What is the molecularity of each reaction in the mechanism?
c.Which step is rate determining? Why?
d. Write the rate law for the net reaction.
a. Adding all of the reactions together and canceling intermediates gives:
[IrCl6]2–(aq) + [W(CN)8]4–(aq) → ← [IrCl6]3–(aq) + [W(CN)8]3–(aq)
b. The first step in the mechanism is bimolecular and the other two steps are unimolecular.
c. The first step is almost certainly rate determining because of the molecularity. The collision that must occur to initiate the reaction is likely to occur much less readily than rearrangement of the electron distribution and associated bond length changes that happens in the intermediates.
d. Since the first step of the mechanism is rate determining, the net rate law is governed by the rate law of the first step:
Rate = k[ [IrCl6]2– ] [ [W(CN)8]4– ]
6. Write the mass action expression for Kc for the following reactions.
a. HI(g) → ←H2(g) + I2(g)
b. CO(g) + H2(g) → ←CH3OH(g)
c. HBr(g) + NH3(g) → ←NH4Br(s)
First, balance the reaction:
2 HI(g) → ← H2(g) + I2(g)
Then, the mass action expression is given by:
Kc = [H2]e[I2]e/[HI]e2
b. First, balance the reaction:
CO(g) + 2 H2(g) → ←CH3OH(g)
Then, the mass action expression is given by:
Kc = [CH3OH]e/[H2]e2[CO]e
c. The reaction is already balanced but the solid product does not contribute to the mass action expression:
Kc = 1/[HCl]e[NH3]e
7. Consider the following set of reactions:
A(g) → ← B(g) Kp = 10
B(g) + C(g) → ← D(g) Kp = 100
D(g) → ← E(g) Kp = 0.1
Find the equilibrium constant for the reaction:
A(g) + E(g) → ← 2 B(g) + C(g)
Find the equilibrium constant for the reaction:
A(g) + E(g) → ← 2 B(g) + C(g)
Write the given reactions in the following manner, adjusting equilibrium constants accordingly:
A(g) → ← B(g) Kp = 10
E(g) → ← D(g) Kp = 1/0.1 = 10
D(g) → ← B(g) + C(g) Kp = 1/100 = 0.01
Adding all of the reactions together gives the target reaction. To find the equilibrium constant for the net reaction, use the Law of Multiple Equilibria and multiply the individual equilibrium constants:
Kp = 10 × 10 × 0.01 = 1