 Exam 1B, Spring 2002
Exam 1B, Spring 2002 Exam 1B, Spring 2002
Exam 1B, Spring 20021. Bromate ion reacts with solid iodine molecules to give liquid bromine molecules and iodate ions. The rate of loss of bromate ions under some conditions is found to be 1×103 mol/L/s.
a) Under the same conditions, what is the rate of loss of iodine molecules?
b) Under the same conditions, what is the rate of gain of iodate ions?
2 BrO3–(aq) + I2(s) → Br2(l) + 2 IO3–(aq)
a) Based on the stoichiometry, the rate of loss of iodine is half the rate of loss of the bromate:
Rate(I2 loss) = –5×102 mol/L/s
b) Under the same conditions, what is the rate of gain of iodate ions?
There is a 1:1 stoichiometry between bromate and iodate, so:
Rate(iodate gain) = 1×103 mol/L/s
2. Hypochlorite ion reacts with iodide ion in the presence of hydroxide to give hypoiodite ion and chloride ion. The following data was found:
[hypochlorite] (M) [iodide] (M) [hydroxide] (M) Initial Rate (mol/L/s)
1.00 1.00 1.00 60
2.00 1.00 1.00 120
1.00 2.00 1.00 120
1.00 1.00 2.00 30
a) Find the rate law.
b) Find the rate constant and give the units.
a) Doubling hypochlorite doubles the rate, which implies first order in [OCl–]
Doubling iodide doubles the rate, which implies first order in [I–]
Doubling hydroxide halves the rate, which implies –1 order in [OH–]
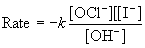
b) Using the concentrations from the first experiment gives k = 60 s–1
3. Rate constants were measured for some reaction at several temperatures and the following plots were made:
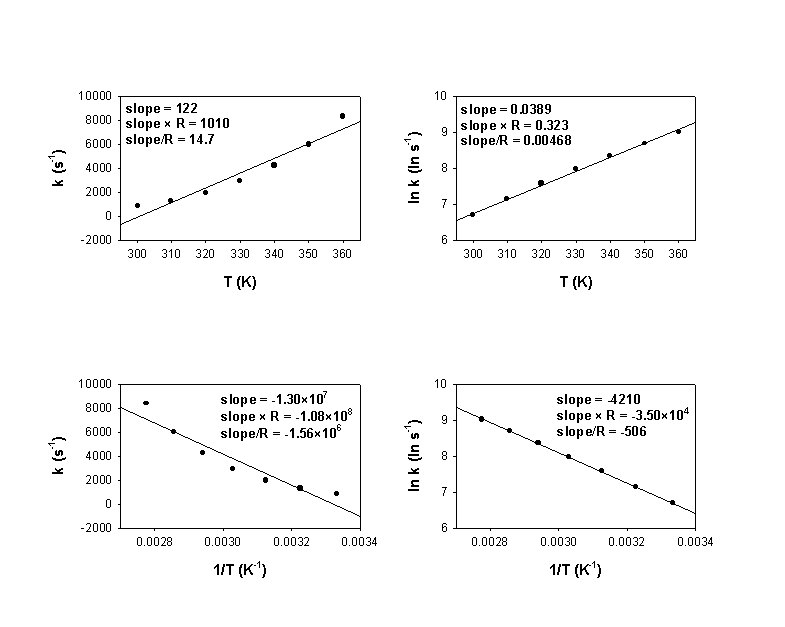
a) What is the activation energy for the reaction in units of kJ/mol?
b) What is the order of the reaction? Why?
a) Activation energies are found from the lnk vs. 1/T plot:
Ea = –slope×R = –3.50×104
Ea = 3.50×104 J/mol = 35.0 kJ/mol
b) What is the order of the reaction? Why?
This is first order reaction, based on the units of the rate constant.
4. Write the mass action expressions for Kp for the following reactions:
a) N2(g) + O2(g) → ← N2O4(g)
b) KClO3(s) → ← KCl(s) + O2(g)
c) Cl2(g) + Br2(g) → ← BrCl3(g)
a) 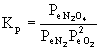
b) 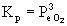
c) 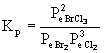
5. The following mechanism was proposed for the reaction between hydrogen and nitrogen to give ammonia:
H2(g) + Fe(s) → FeH2(s)
FeH2(s) + N2(g) 7rarr; Fe(s) + N2H2(g)
FeH2(s) + N2H2(g) → Fe(s) + N2H4(g)
FeH2(s) + N2H4(g) → Fe(s) + 2 NH3(g)
a) The mechanism is incomplete because it does not match the reaction stoichiometry. Correct the problem and write the net reaction.
b) What is the molecularity of each reaction in the mechanism?
c) The reaction has a higher rate when iron powder is used rather than a block of iron. Why?
d) The reaction also proceeds in the absence of iron. What experimental modification would be required to maintain the rate if iron were removed from the reaction mixture?
a) The mechanism is incomplete because it does not match the reaction stoichiometry. Correct the problem and write the net reaction.
The first reaction needs to be tripled so all of the intermediates can be eliminated:
3 H2(g) + 3 Fe(s) → 3 FeH2(s)
Net: 3 H2(g) + N2(g) → 2 NH3(g)
b) Each reaction in the mechanism is bimolecular.
c) Powdered iron has a higher surface area, allowing more interaction with the reactants.
d) Iron acts as a catalyst. Removing the iron will raise the activation energy, so to maintain the same rate a higher temperature would be required.
6. The following reaction was allowed to come to equilibrium.
ClO2(g) → ← Cl2(g) + O2(g) ΔHo = –102.5 kJ/mole
Which way does the reaction shift if
a) chlorine dioxide is added to the reaction?
b) the temperature is raised?
c) the pressure is increased by reducing the volume of the reaction vessel?
First, the reaction needs to be balanced:
2 ClO2(g) → ← Cl2(g) + 2 O2(g) + heat
a) The reaction shifts right, towards products, to remove some of the added ClO2
b) The reaction shifts left, towards reactants, to remove the added heat
c) The reaction shifts left, towards reactants with fewer moles of gases, to reduce the total pressure
7. Find the equilibrium constant Kc for the reaction:
2A(g) + B(g) → ← G(g) + H(g)
given the following information:
A(g) + B(g) → ← C(g) + D(g) Kc = 1
E(g) + F(g) → ← A(g) + C(g) Kc = ½
D(g) + E(g) → ← G(g) Kc = ½
H(g) → ← F(g) Kc = 4
A(g) + B (g) → ← C(g) + D(g) Kc = 1
A(g) + C(g) → ← E(g) + F(g) Kc = 1/(½) = 2
D(g) + E(g) → ← G(g) Kc = ½
F(g) → ← H(g) Kc = 1/4 = ¼
Sum to give the net reaction:
2 A(g) + B(g) → ← G(g) + H(g) Kc = (1)(2)(½)(¼) = ¼