 Practice Problems
Thermodynamics
Practice Problems
Thermodynamics Practice Problems
Thermodynamics
Practice Problems
Thermodynamics1. Why is the entropy change in a system not always a reliable predictor of whether the process producing the change is spontaneous?
The second law states that a process is spontaneous if the system and the surroundings have an increase in entropy. Thus, even is a given system has a decrease in entropy (suggesting nonspontaneity), if there is sufficient increase in the entropy of the surroundings then the process can be spontaneous.
2. How does the equilibrium constant Keq resemble, and how does it differ from, Kc and Kp?
The thermodynamic equilibrium constant Keq is formally written in terms of activities, a unitless quantity. Activities are approximated by using solution concentrations in units of molarity (divided by 1 M to remove the units) and gas partial pressures in units of atm (divided by 1 atm to remove the units). Kc is written solely in terms of molarity and Kp is written solely in terms of partial pressures. Keq can mix "units".
3. For each of the following reactions, indicate whether you would expect the entropy of the system to increase or decrease. If you cannot tell by inspecting the equation, explain why.
(a) CH3OH(l) → CH3OH(g)
(b) N2O4(g) → 2 NO2(g)
(c) CO(g) + H2O(g) → CO2(g) + H2(g)
(d) 2 KClO3(s) → 2 KCl(s) + 3 O2(g)
(e) CH3COOH(l )→ CH3COOH(s)
(f) N2(g) + O2(g) → 2 NO(g)
(g) N2H4(l) → N2(g) + 2 H2(g)
(h) 2 NH3(g) + H2SO4(aq) → (NH4)2SO4(aq)
(a) CH3OH(l) → CH3OH(g)
The entropy, S, increases because there are more moles of gaseous products.
(b) N2O4(g) → 2 NO2(g)
The entropy, S, increases because there are more moles of gaseous products.
(c) CO(g) + H2O(g) → CO2(g) + H2(g)
Can not predict the entropy change because there are the same number of moles of gaseous products and reactants.
(d) 2 KClO3(s) → 2 KCl(s) + 3 O2(g)
The entropy, S, increases because there are more moles of gaseous products.
(e) CH3COOH(l)→CH3COOH(s)
ΔS° < 0 (decrease in entropy) since the reaction goes from a liquid to a solid.
(f) N2(g) + O2(g)→2 NO(g)
ΔS° ~ 0 (little change in entropy) since the reaction goes from 2 moles of gases to 2 moles of gases.
(g) N2H4(l)→N2(g) + 2 H2(g)
ΔS° > 0 (increase in entropy) since the reaction goes from a liquid to a 3 moles of gases.
(h) 2 NH3(g) + H2SO4(aq) → (NH4)2SO4(aq)
ΔS° < 0 (decrease in entropy) since the reaction goes from a liquid + 2 moles of gases to an all liquid state.
4. Based on a consideration of entropy changes, why is it so difficult to eliminate environmental pollution such as the contamination of groundwater with water-soluble methyl tert-butyl ether?
Pollution is caused by random and widespread disposal of items, a high entropy situation. To eliminate pollution, the reverse process must be invoked, so that the entropy of the system now becomes negative, which requires and large positive entropy change for the surroundings and a large energy input.
5. Would you expect each of the following reactions to be spontaneous at low temperatures, high temperatures, all temperatures, or not at all? Explain.
(a) PCl3(g) + Cl2(g) → PCl5(g) ΔH° = –87.9 kJ
(b) 2 NH3(g) → N2(g) + 3 H2(g) ΔH° = +92.2 kJ
(c) 2 N2O(g) → 2 N2(g) + O2(g) ΔH° = –164.1 kJ
(d) H2O(g) + ½O2(g) → H2O2(g)ΔH° = +105.5 kJ
(e) CH4(g) + O2(g) → CO2(g) + 2 H2O(g)ΔH° = –802.3 kJ
(f) 2 CO(g) + O2(g) → 2 CO2(g)ΔH° = –566.0 kJ
(a) PCl3(g) + Cl2(g) → PCl5(g) ΔH° = –87.9 kJ
ΔS° is predicted to be negative since there are fewer moles of gaseous products than reactants. Thus, at low temperatures enthalpy will dominate (TΔS° is small) and the reaction will be spontaneous (ΔH° < 0) while at high temperature the entropy dominates and the reaction becomes nonspontaneous (TΔS° becomes large and negative).
(b) 2 NH3(g) → N2(g) + 3 H2(g) ΔH° = +92.2 kJ
ΔS° is predicted to be positive since there are more moles of gaseous products than reactants. Thus, at low temperatures enthalpy will dominate (TΔS° is small) and the reaction will be nonspontaneous (ΔH° > 0) while at high temperature the entropy dominates and the reaction becomes spontaneous (TΔS° becomes large and positive).
(c) 2 N2O(g) → 2 N2(g) + O2(g) ΔH° = –164.1 kJ
ΔS° is predicted to be positive since there are more moles of gaseous products than reactants. Thus, at low temperatures enthalpy will dominate (TΔS° is small) and the reaction will be spontaneous (ΔH° < 0) while at high temperature the entropy dominates and the reaction is also spontaneous (TΔS° becomes large and positive). Therefore, the reaction is expected to be spontaneous over all temperatures.
(d) H2O(g) + ½O2(g) → H2O2(g) ΔH° = +105.5 kJ
ΔS° will be negative (1.5 moles gases in reactants but only 1 mole of gases in the product) and ΔH° is positive so ΔG° will be positive at all temperatures. Thus, the reaction is never spontaneous.
(e) CH4(g) + O2(g) → CO2(g) + 2 H2O(g) ΔH° = –802.3 kJ
ΔS° will be positive (2 moles gases in reactants but 3 moles of gases in the product) and ΔH° is negative so ΔG° will be negative at all temperatures. Thus, the reaction is spontaneous at all temperatures.
(f) 2 CO(g) + O2(g) → 2 CO2(g) ΔH° = –566.0 kJ
ΔS° will be negative (3 moles gases in reactants but only 2 moles of gases in the product) and ΔH° is negative so ΔG° will be negative at low temperatures and positive at high temperatures. Thus, the reaction is spontaneous only at low temperature.
6. Use the data from the Table of Thermodynamic Quantities to determine ΔG° values for the following reactions at 25 °C.
(a) C2H4(g) + H2(g) → C2H6(g)
(b) SO3(g) + CaO(s) → CaSO4(s)
(a) C2H4(g) + H2(g) → C2H6(g)
ΔGf°(C2H6(g)) = –32.89 kJ/mol
ΔGf°(H2(g)) = 0.00 kJ/mol
ΔGf°(C2H4(g)) = 68.12 kJ/mol
so ΔG° = [–32.89] – [68.12 + 0.00] = –101.01 kJ
(b) SO3(g) + CaO(s) → CaSO4(s)
ΔGf°(CaSO4(s)) = –1322 kJ/mol
ΔGf°(CaO(s)) = –604.0 kJ/mol
ΔGf°(SO3(g)) = –371.1 kJ/mol
so ΔG° = [–1322] – [–604.0 + –371.1] = –347 kJ
7. Use the data from the Table of Thermodynamic Quantities to determine ΔH° and ΔS°, at 298 K, for the following reaction. Then determine ΔG° in two ways, and compare the results.
CS2(l) + 3 O2(g) → CO2(g) + 2 SO2(g)
The enthalpy of reaction is found from the enthalpies of formation:
ΔHf° (CS2(l)) = 89.70 kJ/mol
ΔHf° (O2(g)) = 0 kJ/mol
ΔHf° (CO2(g)) = –393.5 kJ/mol
ΔHf° (SO2(g)) = –296.8 kJ/mol
ΔH° = [(–393.5) + 2(–296.8)] – [(89.70) + 3(0)] = –1076.8 kJ
The entropy of reaction is found from the standard entropies:
S° (CS2(l)) = 151.3 J/mol·K
S° (O2(g)) = 205.0 J/mol·K
S° (CO2(g)) = 213.6 J/mol·K
S° (SO2(g)) = 248.1 J/mol·K
ΔS° = [(213.6) + 2(248.1)] – [(151.3) + 3(205.0)] = –56.5 J/K
One way to find ΔG° is to use the free energies of formation:
ΔGf° (CS2(l)) = 65.27 kJ/mol
ΔGf° (O2(g)) = 0 kJ/mol
ΔGf° (CO2(g)) = –394.4 kJ/mol
ΔGf° (SO2(g)) = –300.2 kJ/mol
ΔG° = [(–394.4) + 2(–300.2)] – [(65.27) + 3(0)] = –1060.1 kJ
Another way to find the free energy of reaction is to use the enthalpy and entropy changes:
ΔG° = ΔH° – TΔS° = –1076.8 – (298)( –0.0565) = –1060.0 kJ
As required, the Gibb's free energies are the same, within experimental error.
8. Use data from the Table of Thermodynamic Quantities to determine ΔH° and ΔS°, at 298 K, for the following reaction. Then determine ΔG° in two ways and compare the results.
C(graphite) + H2O(g) → CO(g) + H2(g)
C(graphite)
ΔHf° = 0.00 kJ/mol
S° = 5.74 J/mol·K
ΔGf° = 0.00 kJ/mol
H2O(g)
ΔHf° = –241.8 kJ/mol
S° = 188.7 J/mol·K
ΔGf° = –228.6 kJ/mol
CO(g)
ΔHf° = –110.5 kJ/mol
S° = 197.6 J/mol·K
ΔGf° = –137.2 kJ/mol
H2(g)
ΔHf° = 0.00 kJ/mol
S° = 130.6 J/mol·K
ΔGf° = 0.00 kJ/mol
ΔH° = [–110.5 + 0.0] – [0.0 + –241.8] = 131.3 kJ
ΔS° = [197.6 + 130.6] – [5.74 + 188.7] = 133.8 J/K = 0.1338 kJ/K
ΔG° = [–137.2 + 0.0] – [0.0 + –228.6] = 91.4 kJ
ΔG° = 131.3 – (298)(0.1338) = 91.4 kJ
Both methods give the same ΔG°, as indeed they should.
9. Estimate the normal boiling of heptane, C7H16, given that at this temperature ΔH°vapn = 31.69 kJ/mol.
Use Trouton's Rule: ΔS°vpn = ΔH°vpn/Tbp ≈ 87 J/mol·K
so Tbp = ΔH°vapn/(87 J/mol·K) = (31690 J/mol)/(87 J/mol·K) = 364 K = 91 °C.
10. The normal boiling point of Br2(l) is 59.47 °C. Estimate ΔH°vapn of bromine. Compare your result with a value based on data from the Table of Thermodynamic Quantities.
Trouton's Rule suggests that ΔH°vapn = 87 J/mol·K×Tbp = (87)(273.15 + 59.47) = 29000 J/mol = 29 kJ/mol.
To use the data from the Table of Thermodynamic Quantities, use the reaction:
Br2(l) → Br2(g)
with ΔHf° (Br2(l)) = 0 kJ/mol and ΔHf° (Br2(l)) = 30.91 kJ/mol so ΔH° = ΔH°vapn = [30.91] – [0] = 30.91 kJ/mol.
Given the approximate nature of Trouton's Rule, the estimate and the experimental value are remarkably similar.
11. Write Keq expressions for the following reactions. Which, if any, of these expressions correspond to equilibrium constants that we have previously denoted as Kc, Kp, Ka, and so on?
(a) 2 NO(g) + O2(g) → ← 2 NO2(g)
(b) MgSO3(s) → ← MgO(s) + SO2(g)
(c) HCN(aq) + H2O(l) → ← H3O+(aq) + CN–(aq)
(a) 2 NO(g) + O2(g) → ← 2 NO2(g)
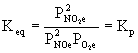
(b) MgSO3(s) → ← MgO(s) + SO2(g)

(c) HCN(aq) + H2O(l) → ← H3O+(aq) + CN–(aq)

12. Use the data from the Table of Thermodynamic Quantities to determine Kp at 298 K for these reactions.
(a) 2 SO2(g) + O2(g) → ← 2 SO3(g)
(b) CH4(g) + 2 H2O(g) → ← CO2(g) + 4 H2(g)
(a) 2 SO2(g) + O2(g) → ← 2 SO3(g)
ΔGf° (SO3(g)) = –371.1 kJ/mol
ΔGf° (SO2(g)) = –300.2 kJ/mol
ΔGf° (O2(g)) = 0 kJ/mol
ΔG° = [2(–371.1)] – [2(–300.2) + (0)] = –141.8 kJ
ΔG° = –RTlnKp
–141800 = –(8.314)(298)lnKp
Kp = e57.23 = 7.2×1024
(b) CH4(g) + 2 H2O(g) → ← CO2(g) + 4 H2(g)
ΔGf° (CO2(g)) = –394.4 kJ/mol
ΔGf° (H2(g)) = 0 kJ/mol
ΔGf° (CH4(g)) = –50.75 kJ/mol
ΔGf° (H2O(g)) = –228.6 kJ/mol
ΔG° = [(–394.4) + 4(0)] – [(–50.75) + 2(–228.6)] = 113.6 kJ
ΔG° = –RTlnKp
113600 = –(8.314)(298)lnKp
Kp = e–45.85 = 1.2×10–20
13. Use data from the Table of Thermodynamic Quantities to determine Kp at 298 K for these reactions.
(a) 2 N2O(g) + O2(g) → ← 4 NO(g)
(b) 2 NH3(g) + 2 O2(g) → ← N2O(g) + 3 H2O(g)
(a) 2 N2O(g) + O2(g) → ← 4 NO(g)
ΔG°f(NO(g)) = 86.57 kJ/mol
ΔG°f(O2(g)) = 0.00 kJ/mol
ΔG°f(N2O(g)) = 104.2 kJ/mol
ΔG° = [4(86.57)] – [2(104.2) + 0.0] = 137.9 kJ
137900 = –(8.314)(298)lnKp
lnKp = –55.7
Kp = e–55.7 = 6×10–25
(b) 2 NH3(g) + 2 O2(g) → ← N2O(g) + 3 H2O(g)
ΔG°f(N2O(g)) = 104.2 kJ/mol
ΔG°f(H2O(g)) = –228.6 kJ/mol
ΔG°f(NH3(g)) = –16.48 kJ/mol
ΔG°f(O2(g)) = 0.00 kJ/mol
ΔG° = [104.2 + 3(–228.6)] – [2(–16.48) + 2(0.00)] = –548.6 kJ
–548600 = –(8.314)(298)lnKp
lnKp = 221.4
Kp = e221.4 = 1×1096
14. The thermodynamic data listed below are for 298 K. Use these data and data from the Table of Thermodynamic Quantities to determine Keq at 45 °C for the reaction
CO2(g) + SF4(g) → ← CF4(g) + SO2(g)
ΔHf°, kJ/mol S°, J mol–1 K–1
SF4(g) –763 299.6
CF4(g) –925 261.6
Find the enthalpy of reaction at 298 K:
ΔHf°(CF4(g)) = –925 kJ/mol
ΔHf°(SO2(g)) = –296.8 kJ/mol
ΔHf°(SF4(g)) = –763 kJ/mol
ΔHf°(CO2(g)) = –393.5 kJ/mol
ΔH° = [(–925) + (–296.8)] – [(–393.5) + (–763)] = –65 kJ
Find the entropy of reaction at 298 K:
S°(CF4(g)) = 261.6 J/mol·K
S°(SO2(g)) = 248.1 J/mol·K
S°(SF4(g)) = 299.6 J/mol·K
S°(CO2(g)) = 213.6 J/mol·K
ΔS° = [(261.6) + (248.1)] – [(213.6) + (299.6)] = –3.5 J/K
Assuming that ΔH° and ΔS° do not change significantly between 298 K and 318 K (45 °C):
ΔG° = ΔH° – TΔS° = –65 – (318)(–0.0035) = –64 kJ = –64000 J
ΔG° = –RTlnKeq
–64000 = –(8.314)(318)lnKeq
Keq = e24.2 = 3×1010
15. The following reaction is carried out on an industrial scale for the production of thionyl chloride, a chemical used in the manufacture of pesticides.
SO3(g) + SCl2(l) → ← OSCl2(l) + SO2(g)
The thermodynamic data listed below are for 298 K. Use these data and data from the Table of Thermodynamic Quantities to determine the temperature at which Keq = 1.0×1015 for the reaction.
ΔHf°, kJ/mol S°, J mol–1 K–1
SCl2(l) –5.0 184
OSCl2(l) –245.6 121
ΔH°f(SO2(g)) = –296.8 kJ/mol
ΔH°f(SO3(g)) = –395.7 kJ/mol
ΔH°f(SCl2(g)) = –50.0 kJ/mol
ΔH°f(OSCl2(g)) = –245.6 kJ/mol
ΔH° = [–245.6 + –296.8] – [–395.7 + –50.0] = –96.7 kJ
S°(SO2(g)) = 248.1 J/mol·K
S°f(SO3(g)) = 256.6 J/mol·K
S°f(SCl2(g)) = 184 J/mol·K
S°f(OSCl2(g)) = 121 J/mol·K
ΔS° = [121 + 248.1] – [256.6 + 184] = –72 J/K
–(8.314)Tln(1.0×1015) = –96700 – T(–72)
–287T = –96700 + 72T
–359T = –96700
T = 269 K (= –4 °C)
16. On several occasions, we have made the assumption that ΔH° and ΔS° undergo little change with temperature. Why can we not make the same assumption about ΔG°? If we assume that ΔH°298 and ΔS°298 do not change with temperature, is it possible for a reaction that is nonspontaneous under standard-state conditions to become spontaneous both at some higher temperature and some lower temperature? Explain.
Since ΔG° = ΔH° – TΔS°, the Gibb's energy changes linearly with temperature. If ΔS° is a large value, then ΔG° can change significantly with temperature.
If the enthalpy change and the entropy change are both constant with respect to temperature and a reaction is nonspontaneous at standard-state conditions, the reaction can not become spontaneous both at higher and lower temperature. For example, if both the enthalpy change and the entropy change are negative, the reaction could be nonspontaneous at standard-state conditions and could become spontaneous at lower temperature; however, this scenario does not allow spontaneity at higher temperature (the Gibb's energy change is always positive after a certain temperature is attained).
17. Following are values of Kp at different temperatures for the reaction, 2 SO2(g) + O2(g) → ← 2 SO3(g).
At 800 K, Kp = 9.1×102; at 900 K, Kp = 4.2×101; at 1000 K, Kp = 3.2; at 1100 K, Kp = 0.39; and at 1170 K, Kp = 0.12. Construct a plot to determine ΔH° for this reaction.
The van't Hoff equation is 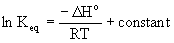 so the slope of the ln Keq versus 1/T
plot equals –ΔH°/R.
so the slope of the ln Keq versus 1/T
plot equals –ΔH°/R.
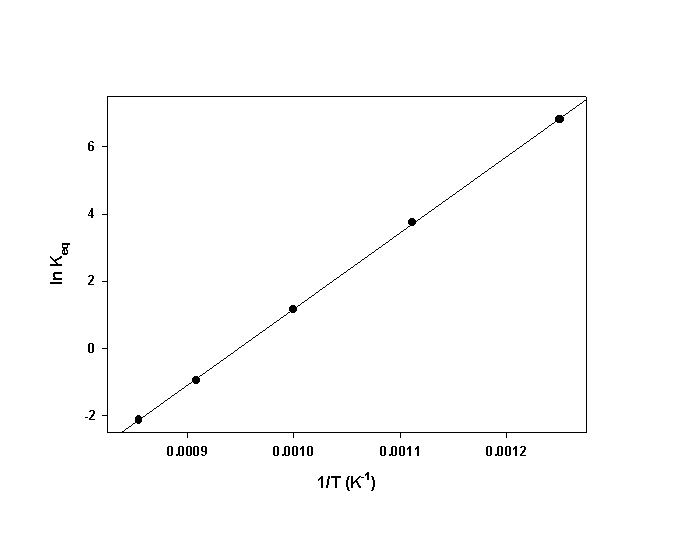
The slope of the plot = 22700 so ΔH° = –R×slope = –(8.314)×(22700) = –189000 J/mol = –189 kJ/mol
18. Use thermodynamic data to determine Keq for the following reaction
Mg(OH)2(s) + 2 NH4+(aq) → ← Mg2+(aq) + 2 NH3(aq) + 2 H2O(l)
Then obtain Keq from other tabulated equilibrium constants and compare the results.
ΔGf° (Mg2+(aq)) = –454.8 kJ/mol
ΔGf° (NH3(aq)) = –26.57 kJ/mol
ΔGf° (H2O(l)) = –237.2 kJ/mol
ΔGf° (NH4+(aq)) = –79.31 kJ/mol
ΔGf° (Mg(OH)2(s)) = –833.9 kJ/mol
ΔG° = [(–454.8) + 2(–26.57) +2(–237.2)] – [(–833.9) + 2(–79.31)] = 10.2 kJ
ΔG° = –RTlnKeq
10200 = –(8.314)(298)lnKeq
Keq = e–4.12 = 1.6×10–2
To use published equilibrium constants, a series of reactions must be used:
Mg(OH)2(s) → ← Mg2+(aq) + 2 OH–(aq)Ksp = 1.8×10–11
NH4+(aq) + H2O(l) → ← H3O+(aq) + NH3(aq) Ka = 5.6×10–10
NH4+(aq) + H2O(l) → ← H3O+(aq) + NH3(aq) Ka = 5.6×10–10
H3O+(aq) + OH–(aq) → ← 2 H2O(l) Kc = 1/Kw = 1/1.0×10–14 = 1.0×1014
H3O+(aq) + OH–(aq) → ← 2 H2O(l)Kc = 1/Kw = 1/1.0×10–14 = 1.0×1014
Summing the reactions gives the desired reaction with
Kc = Ksp×Ka×Ka×1/Kw×1/Kw = (1.8×10–11)(5.6×10–10)(5.6×10–10) (1.0×1014)(1.0×1014) = 5.6×10–2
The two equilibrium constants are the same order of magnitude, but differ by about a factor of 3.5. This is not too bad.
19. Use thermodynamic data to obtain a value of Ksp for Ag2SO4, and compare your result with the one found in the table of solubility product constants.
The reaction is:
Ag2SO4(s) → ← 2 Ag+(aq) + SO42–(aq)
ΔG°f(SO42–) = –744.5 kJ/mol
ΔG°f(Ag+) = 77.11 kJ/mol
ΔG°f(Ag2SO4) = –618.5 kJ/mol
ΔG° = [2(77.11) + –744.5] – [–618.5] = 28.2 kJ
ΔG° = –RTln Keq = –RTlnKsp
28200 = –(8.314)(298)ln Ksp
ln Ksp = –11.4
Ksp = e–11.4 = 1×10–5
From the Table, Ksp = 1.4×10–5; the two values are the same, within error.