 Practice Problems
Acids & Bases
Practice Problems
Acids & Bases Practice Problems
Acids & Bases
Practice Problems
Acids & Bases1. Write equations to represent the ionization of HI as an acid in both the Arrhenius and Brønsted-Lowry theories.
HI is a strong acid, so will ionize completely.
In Arrhenius theory, the acid dissociates into a hydrogen ion and the anion. For HI, then:
HI(aq) → H+(aq) + I–(aq)
In Brønsted-Lowry theory, the acid is a hydrogen ion donor and another species is required to act as the hydrogen ion acceptor. In aqueous solution, the hydrogen ion acceptor is water, so:
HI(aq) + H2O(l) → H3O+(aq) + I–(aq)
2. Write equations for the ionizations and Ka expressions for each of the following Brønsted-Lowry weak acids.
(a) HOClO
(b) CH3CH2COOH
(c) HCN
(d) C6H5OH
(a) HOClO
HOClO(aq) + H2O(l) → ← H3O+(aq) + OClO–(aq)
(b) CH3CH2COOH
CH3CH2COOH(aq) + H2O(l) → ← H3O+(aq) + CH3CH2COO–(aq)
(c) HCN
HCN(aq) + H2O(l) → ← H3O+(aq) + CN–(aq)
(d) C6H5OH
C6H5OH(aq) + H2O(l) → ← H3O+(aq) + C6H5O–(aq)
3. Explain how the strengths of
(a) binary acids are affected by bond energies and the ionic radii of the anions they produce
(b) oxoacids are affected by the electronegativity of the central nonmetal atom and the number of terminal O atoms
(a) The bond energy of the H-X bond is directly related to the acid strength. If the H-X bond is weak, then the bond is easily broken and gives a stronger acid. If the bond is strong, then it is difficult to break the bond, that is difficult to donate H+, so is a weaker acid. Anions with large ionic radii are the conjugate base of strong acids. If an anion has a large ionic radius, then the HX bond formed will be relatively long. Long bonds give small bond energies, which leads to strong acids. Small anionic radii lead to short and strong bonds, which is the description of a weak acid.
(b) The central atom (if it is more electronegative than H) and terminal oxygen atoms draw electron density away from the hydrogen atoms; this makes the H atoms more H+ - like, thus a stronger acid.
4. For each of the following, identify the conjugate acid-base pairs.
(a) HOClO2(aq) + H2O(l) → ← H3O+(aq) + OClO2–(aq)
(b) HSeO4–(aq) + NH3(aq) → ← NH4+(aq) + SeO42–(aq)
(c) HCO3–(aq) + OH–(aq) → ← CO32–(aq) + H2O(l)
(d) C5H5NH+(aq) + H2O(l) → ← C5H5N(aq) + H3O+(aq)
(a) HOClO2(aq) + H2O(l) → ← H3O+(aq) + OClO2–(aq)
Acid: HOClO2
Base: H2O
Conjugate Acid: H3O+
Conjugate Base: OClO2–
(b) HSeO4–(aq) + NH3(aq) → ← NH4+(aq) + SeO42–(aq)
Acid: HSeO4–
Base: NH3
Conjugate Acid: NH4+
Conjugate Base: SeO42–
(c) HCO3–(aq) + OH–(aq) → ← CO32–(aq) + H2O(l)
Acid: HCO3–
Base: OH–
Conjugate Acid: CO32–
Conjugate Base: H2O
(d) C5H5NH+(aq) + H2O(l) → ← C5H5N(aq) + H3O+(aq)
Acid: C5H5NH+
Base: H2O
Conjugate Acid: H3O+
Conjugate Base: C5H5N
5. Phenol, C6H5OH, used as a disinfectant and in the manufacture of plastics, dyes, and indicators, ionizes as an acid.
C6H5OH(aq) + H2O(l) → ← H3O+(aq) + C6H5O–(aq)
Ka = 1.0×10–10
Arrange the following substituted phenols in the order in which you would expect their Ka values to increase. Where would you expect phenol itself to fit into this ranking?
(a) 3-chlorophenol
(b) 2,4-dichlorophenol
(c) 2,4,6-trichlorophenol
(d) 4-chlorophenol
The acid strength will change depending upon the relative electronegativity experienced by the ionizable hydrogen atom. All of these examples are substituted by Cl atoms, which have a high electronegativity. The general trend will be determined by first, the number of Cl atoms (more Cl atoms will give more total electroneagtivity), and second, by the location of the Cl atom relative to the ionizable H atom (a closer Cl atom withdraws more electron density from the H atom than a more remote Cl atom). Using these principals:
2,4,6-Trichlorophenol has three electronegative chlorine atoms so is the most acidic. 2,4-Dichlorophenol has two Cl atoms, so is next. 3-Chlorophenol and 4-Chlorophenol both have only a single Cl atom but in 4-chlorophenol the Cl atom is farther from the H atom, so is the least acidic. Phenol is less acidic than any of these because it has no electronegative Cl atoms.
Net: (least acidic) phenol < 4-chlorophenol < 3-chlorophenol < 2,4-dichlorophenol < 2,4,5-trichlorophenol
6. What is the pH of each of the following aqueous solutions?
(a) 0.039 M HCl
(b) 0.070 M KOH
(c) 0.65 M HBr
(d) 2.5×10–4 M Ca(OH)2
Assume 25 °C in all cases. Write out the reactions in order to find the [H3O+] or [OH–] concentration for each acid or base. Then use the definitions pH = –log[H3O+] or pOH = –log[OH–] and the relation pH + pOH = 14.00 (only true at 25 °C). Note that these are all strong acids or bases.
(a) 0.039 M HCl
HCl(aq) + H2O(l) → H3O+(aq) + Cl–(aq)
[H3O+] = [HCl] = 0.039
pH = –log[0.039] = 1.41
(b) 0.070 M KOH
KOH(aq) → K+(aq) + OH–(aq)
[OH–] = [KOH] = 0.070
pOH = –log[0.070] = 1.15
pH = 14.00 – pOH = 14.00 – 1.15 = 12.85
(c) 0.65 M HBr
HBr(aq) + H2O(l) → H3O+(aq) + Br–(aq)
[H3O+] = [HBr] = 0.65
pH = –log[0.65] = 0.19
(d) 2.5×10–4 M Ca(OH)2
Ca(OH)2(aq) → Ca2+(aq) + 2 OH–(aq)
[OH–] = 2×[Ca(OH)2] = 2×2.5×10–4 = 5.0×10–4
pOH = –log[5.0×10–4] = 3.30
pH = 14.00 – pOH = 14.00 – 3.30 = 10.70
7. What is the pOH of each of the following aqueous solutions?
(a) 0.073 M LiOH
(b) 1.75 M NaOH
(c) 0.045 M Ba(OH)2
(d) 9.1×10–2 M HClO4
(a) 0.073 M LiOH
LiOH(aq) → Li+(aq) + OH–(aq) (strong base)
0.073 M LiOH = 0.073 M OH–
pOH = –log[OH–] = –log[0.073] = 1.14
(b) 1.75 M NaOH
NaOH(aq) → Na+(aq) + OH–(aq) (strong base)
1.75 M NaOH = 1.75 M OH–
pOH = –log[OH–] = –log[1.75] = 0.243
(c) 0.045 M Ba(OH)2
Ba(OH)2(aq) → Ba2+(aq) + 2 OH–(aq) (strong base)
0.045 M Ba(OH)2 = 2(0.045) M OH– = 0.090 M OH–
pOH = –log[OH–] = –log[0.090] = 1.046
(d) 9.1×10–2 M HClO4
HClO4(aq) + H2O(l) → H3O+(aq) + ClO4–(aq) (strong acid)
9.1×10–2 M HClO4 = 9.1×10–2 M H3O+
pH = –log[H3O+] = –log[9.1×10–2] = 1.041
pOH = 14.00 – pH (assuming 25 °C) = 14.00 – 1.041 = 12.96
Alternatively: [OH–] = Kw/[ H3O+] = 1.0×10–14/9.1×10–2 = 1.1×10–13
pOH = –log[OH–] = –log[1.1×10–13] = 12.96
8. Describe how you would prepare 2.00 L of an aqueous solution having pH = 3.60, if you had a supply of 0.100 M HCl available.
Given that pH = –log[H3O+], the desired concentration of hydronium ion is
[H3O+] = 10–pH = 10–3.60 = 2.5×10–4 M.
Since HCl is a strong acid, i.e., HCl(aq) + H2O(l) → H3O+(aq) + Cl–(aq)
[H3O+] = [HCl] = 0.100 M in the given solution, so this needs to be diluted to obtain the desired concentration.
Recalling Mconc × Vconc = Mdil × Vdil, the amount of 0.100 M HCl required is
Mconc = 0.100 M
Mdil = 2.5×10–4 M
Vdil = 2.00 L
so Vconc = (2.5×10–4 M × 2.00 L)/(0.100 M) = 0.0050 L = 5.0 mL.
Thus to obtain the pH = 3.60 solution, add 5.0 mL of the 0.100 M HCl solution to a 2.00 L volumetric flask and add water to the mark.
9. 9. Which has the lower pH, 0.00048 M H2SO4 or a vinegar solution having pH = 2.42?
The first hydrogen atom in sulfuric acid is 100% ionized but the second is not. However, if the second hydrogen atom also were 100% ionized, then [H3O+] = 2×0.00048 = 0.00096 M giving a pH = –log[H3O+] = –log[0.00096] = 3.02. Thus, the pH for the sulfuric acid solution must be greater than 3.02 so the vinegar solution has the lower pH.
10. Hydrazoic acid, HN3 (pKa = 4.72), is perhaps best known through its sodium salt, sodium azide, NaN3, the gas forming substance in automobile air-bag systems. What molarity of HN3 is required to produce an aqueous solution with pH = 3.10?
Write the balanced equation, write the mass action expression for Ka, find Ka from pKa, set up a table of concentrations, and solve from there.
HN3(aq) + H2O(l) → ← H3O+(aq) + N3–(aq)
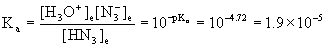
Initial Cinit 0 0
Change – x +x +x
Equilibrium Cinit – x x x
In this case we do not know the initial concentration so we need to find x from some other information: the pH.
x = [H3O+] = 10–pH = 10–3.10 = 7.9×10–4 M
Now we can plug into the mass action expression, knowing the value of x:
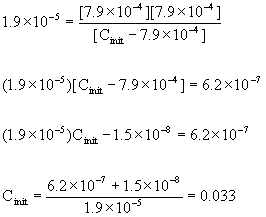
so the initial concentration of HN3 = 0.033 M
11. A 1.00 g sample of aspirin (acetylsalicylic acid) is dissolved in 0.300 L of water at 25 °C, and its pH is found to be 2.62. What is the Ka of aspirin?
o–C6H4(OCOCH3)COOH(aq) + H2O(l) → ← H3O+(aq) + o–C6H4(OCOCH3)COO–(aq)
Ka = ?
Find the molarity of the aspirin sample, use the balanced reaction, write the mass action expression for Ka, set up a table of concentrations, and solve.
o–C6H4(OCOCH3)COOH = C9H8O4 = 9(12.011) + 8(1.008) + 4(15.999) = 180.159 g/mol
initial molarity = (1.00 g/180.159 g/mol)/0.300 L = 0.0185 M
o–C6H4(OCOCH3)COOH(aq) + H2O(l) → ← H3O+(aq) + o–C6H4(OCOCH3)COO–(aq)
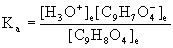
Initial 0.0185 0 0
Change – x +x +x
Equilibrium 0.0185 – x x x
Since Ka is unknown, x must be found from other information, in this case the pH.
x = [H3O+]e = 10–pH = 10–2.62 = 2.4×10–3 M = [C9H7O4–]e
[C9H8O4]e = 0.0185 – 2.4×10–3 = 0.0161 M
These concentrations can be used to find Ka
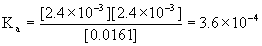
12. Codeine, C18H21NO3, a commonly prescribed painkiller, is a weak base. A saturated aqueous solution contains 1.00 g codeine in 120 mL of solution and has a pH = 9.8. What is the Kb of codeine?
C18H21NO3(aq) + H2O(l) → ← [C18H21NHO3]+(aq) + OH–;(aq)
Kb = ?
Treat this as any equilibrium problem: write the balanced chemical reaction, write the mass action expression for Kb, set up a table of concentrations, and then solve for the unknown variables using the given information. Assume 25 °C.
C18H21NO3(aq) + H2O(l) → ← OH–(aq) + [C18H21NHO3]+(aq)
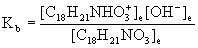
Initial [B]ini 0 0
Change – x +x +x
Equilibrium [B]ini – x x x
[B]ini is found from the concentration information given:
molar mass of codeine = 18(12.01) + 21(1.01) + 1(14.01) + 3(16.00) = 299.4 g/mol
so the molar concentration of the saturated solution is:
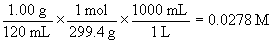
[B]ini = 0.0278 M
The pH gives the hydronium ion concentration:
[H3O+] = 10–pH = 10–9.8 = 2×10–10 M
The hydroxide ion concentration is found from the hydronium ion concentration by:
[OH–] = Kw/[ H3O+] = 1.0×10–14/2×10–10 = 5×10–5 M
Then,
x = [OH–] = 5×10–5 M
[B]ini – x = 0.0278 – 5×10–5 = 0.0278 M
so Kb is found from:
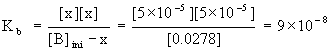
13. Calculate the pH of 0.105 M CCl3COOH (trichloroacetic acid, pKa = 0.52)
Write the reaction, write the mass action expression and find Ka, set up a table of concentrations, plug the equilibrium concentrations into the mass action expression, and then solve.
CCl3COOH(aq) + H2O(l) → ← H3O+(aq) + CCl3COO–(aq)
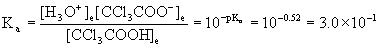
Initial 0.105 0 0
Change – x +x +x
Equilibrium 0.105 – x x x
[HA]init/Ka = 0.105/0.30 = 0.35 < 100 so no approximation
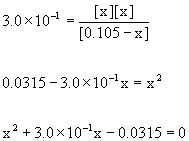
Using the quadratic equation gives
x = –0.38 or x = 0.082; only the positive value makes sense so
x = [H3O+] = 0.082 M
pH = –log[H3O+] = –log[0.082] = 1.09
14. Piperidine, C5H11N (pKb = 2.89), is a colorless liquid having the odor of pepper. Calculate the pH of 0.00250 M C5H11N.
Treat this as any equilibrium problem: write the balanced chemical reaction, write the mass action expression for Kb, set up a table of concentrations, and then solve for the unknown variables using the given information. Assume 25 °C.
C5H11N(aq) + H2O(l) → ← OH–(aq) + C5H11NH+(aq)
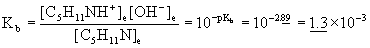
Initial 0.00250 0 0
Change – x +x +x
Equilibrium 0.00250 – x x x
Approximate? 0.00250/1.3×10–3 = 2 < 100 No!
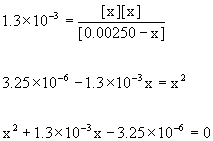
Solve this using the quadratic equation to give:
x = 1.3×10–3, –2.6×10–3
Only the positive root makes sense, so [OH–] = x = 1.3×10–3 M
pOH = –log[OH–] = –log(1.3×10–3) = 2.89
pH = 14.00 – pOH = 14.00 – 2.89 = 11.11
15. For a solution that is 0.15 M H3PO4(aq), determine (a) pH, (b) [H3PO4], (c) [H2PO4–], (d) [HPO42–], and (e) [PO43–].
This is a polyprotic weak acid. The first ionization is treated exactly like every other weak acid:
H3PO4(aq) + H2O(l) → ← H3O+(aq) + H2PO4–(aq)
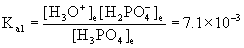
Initial 0.15 0 0
Change – x +x +x
Equilibrium 0.15 – x x x
Approximate? 0.15/7.1×10–3 = 21, NO!
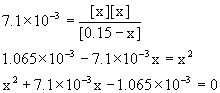
Using the quadratic equation gives
x = 0.029 or x = –0.036
Only the positive value makes sense, so [H3O+] = [H2PO4–] = 0.029 M
[H3PO4] = 0.15 – 0.029 = 0.12 M
The second and third ionizations do not contribute significantly to these concentrations.
To find the hydrogen phosphate concentration, look at the second ionization step:
H2PO4–(aq) + H2O(l) → ← H3O+(aq) + HPO42–(aq)

Initial 0.029 0.029 0
Change – x +x +x
Equilibrium 0.029 – x 0.029 + x x
Approximate? 0.029/6.3×10–8 = 4.6×105, YES!
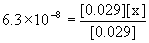
x = [HPO42–] = 6.3×10–8 M
To find the phosphate concentration, look at the third ionization step:
HPO42–(aq) + H2O(l) → ← H3O+(aq) + PO43–(aq)
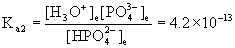
Initial 6.3×10–8 0.029 0
Change – x +x +x
Equilibrium 6.3×10–8 – x 0.029 + x x
Approximate? 6.3×10–8/4.2×10–13 = 1.5×105, YES!
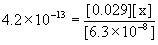
x = [PO43–] = 9.1×10–19 M
Then:
(a) pH = –log[H3O+] = –log[0.029] = 1.54
(b) [H3PO4] = 0.12 M
(c) [H2PO4–] = 0.029 M
(d) [HPO42–] = Ka2 = 6.3×10–8 M
(e) [PO43–] = 9.1×10–19 M
16. Predict whether each of the following solutions is acidic, basic, or neutral. Write balanced equation(s) for any hydrolysis reaction(s) that occur.
(a) RbClO4(aq)
(b) CH3CH2NH3Br(aq)
(c) HCOONH4(aq)
(a) RbClO4(aq)
RbClO4(aq) → Rb+(aq) + ClO4–(aq)
Rb+ is the cation of a strong base (RbOH) so no cation hydrolysis occurs.
ClO4– is the anion of a strong acid (HClO4) so no anion hydrolysis occurs.
Since no hydrolysis occurs, the solution will be neutral.
(b) CH3CH2NH3Br(aq)
CH3CH2NH3Br(aq) → CH3CH2NH3+(aq) + Br–(aq)
CH3CH2NH3+ is the cation of a weak base, CH3CH2NH2, hydrolysis occurs:
CH3CH2NH3+(aq) + H2O(l) → ← H3O+(aq) + CH3CH2NH2(aq)
Br– is the anion of a strong acid (HBr) so no anion hydrolysis occurs:
Since hydronium ion is formed by the cation hydrolysis, the solution will be acidic.
(c) HCOONH4(aq)
HCOONH4(aq) → NH4+(aq) + HCOO–(aq)
NH4+(aq) + H2O(l) → ← H3O+(aq) + NH3(aq)
HCOO– is the anion of a weak acid, HCOOH, so anion hydrolysis occurs:
HCOO–(aq) + H2O(l) → ← HCOOH(aq) + OH–(aq)
The equilibrium constant for the cation hydrolysis is 1.0×10–14/1.8×10–5 = 5.6×10–10.
The equilibrium constant for the anion hydrolysis is 1.0×10–14/1.8×10–4 = 5.6×10–11.
The equilibrium reaction with the larger equilibrium constant will be favored, so the cation hydrolysis dominates, so that more hydronium ion will be formed than hydroxide ion and the solution will be acidic.
17. Predict whether each of the following solutions is acidic, basic, or neutral. Write balanced equation(s) for any hydrolysis reaction(s) that occur.
(a) CH3CH2COOK(aq)
(b) Mg(NO3)2(aq)
(c) NH4CN(aq)
(a) CH3CH2COOK(aq)
CH3CH2COOK(aq) → K+(aq) + CH3CH2COO–(aq)
K+ is the cation of a strong base (RbOH) so no cation hydrolysis occurs.
CH3CH2COO– is the anion of a weak acid (CH3CH2COOH) so anion hydrolysis occurs.
CH3CH2COO–(aq) + H2O(l) → ← OH–(aq) + CH3CH2COOH(aq)
Since hydroxide ion is formed by the anion hydrolysis, the solution will be basic.
(b) Mg(NO3)2(aq)
Mg(NO3)2(aq) → Mg2+(aq) + 2 NO3–(aq)
Mg2+ is the cation of a strong base (Mg(OH)2) so no cation hydrolysis occurs.
NO3– is the anion of a strong acid (HNO3) so no anion hydrolysis occurs.
Since no hydrolysis occurs, the solution will be neutral.
(c) NH4CN(aq)
NH4CN(aq) → NH4+(aq) + CN–(aq)
NH4+(aq) + H2O(l) → ← H3O+(aq) + NH3(aq)
CN– is the anion of a weak acid, HCN, so anion hydrolysis occurs:
CN–(aq) + H2O(l) → ← HCN(aq) + OH–(aq)
The equilibrium constant for the cation hydrolysis is 1.0×10–14/1.8×10–5 = 5.6×10–10.
The equilibrium constant for the anion hydrolysis is 1.0×10–14/6.2×10–10 = 1.6×10–5.
The equilibrium reaction with the larger equilibrium constant will be favored, so the anion hydrolysis dominates, so that less hydronium ion will be formed than hydroxide ion and the solution will be basic.
18. Which of the following 0.100 M solutions has the lowest pH: (a) NaNO3, (b) CH3COOK, (c) NH4I, or (d) Na3PO4?
Hydrolysis occurs by the reaction of water with the conjugate species of weak acids or weak bases.
(a) NaNO3(aq) → Na+(aq) + NO3–(aq)
(Sodium salts and nitrates are freely soluble in water, so the reaction goes to completion.)
Na+ is the conjugate acid of NaOH, a strong base, so does not hydrolyze, i.e.
Na+(aq) + H2O(l) → No Reaction
NO3– is the conjugate base of HNO3, a strong acid, so also does not hydrolyze, i.e.,
NO3– (aq) + H2O(l) → No Reaction
Thus, the solution is neutral, pH ~ 7.
(b) CH3COOK(aq) → K+(aq) + CH3COO–(aq)
(Potassium salts and acetates are freely soluble in water, so the reaction goes to completion.)
K+ is the conjugate acid of KOH, a strong base, so does not hydrolyze, i.e.
K+(aq) + H2O(l) → No Reaction
CH3COO– is the conjugate base of CH3COOH, a weak acid (acetic acid), so does hydrolyze, i.e.
CH3COO–(aq) + H2O(l) → ← CH3COOH(aq) + OH–(aq)
The solution generates hydroxide, so pH > 7.
(c) NH4I(aq) → NH4+(aq) + I–(aq)
(Ammonium salts and most halides are freely soluble in water, so the reaction goes to completion.)
NH4+ is the conjugate acid of NH3, a weak base (ammonia), so does hydrolyze, i.e.
NH4+(aq) + H2O(l) → ← NH3(aq) + H3O+(aq)
I– is the conjugate base of a strong acid, HI, so does not hydrolyze, i.e.
I–(aq) + H2O(l) → No Reaction
The solution generates hydronium ion, so pH < 7.
(d) Na3PO4(aq) → 3 Na+(aq) + PO43– (aq)
(Sodium salts are freely soluble in water, so the reaction goes to completion.)
Na+ is the conjugate acid of NaOH, a strong base, so does not hydrolyze, i.e.
Na+(aq) + H2O(l) → No Reaction
PO43– is the conjugate base of HPO42–, a weak acid, so does hydrolyze, i.e.
PO43– (aq) + H2O(l) → ← HPO42– (aq) + OH–(aq)
The solution generates hydroxide, so pH > 7.
The only acidic solution is (c) so has the lowest pH.
19. For a solution that is 0.080 M NaOCl, (a) write an equation for the hydrolysis that occurs, and determine (b) the equilibrium constant for this hydrolysis and (c) the pH.
(a) NaOCl is a soluble salt, so NaOCl(aq) → Na+(aq) + OCl–(aq)
Na+ is the conjugate acid of a strong base, NaOH, so does not hydrolyze, i.e.
Na+(aq) + H2O(l) → No Reaction
OCl– is the conjugate base of a weak acid, HOCl, so does hydrolyze, i.e.
OCl–(aq) + H2O(l) → ← HOCl(aq) + OH–(aq)
The solution will be basic.
(b) The equilibrium constant is found from the hydrolysis reaction.
OCl–(aq) + H2O(l) → ← HOCl(aq) + OH–(aq)
and has the form of a Kb, which must be found from the Ka of the conjugate acid HOCl:
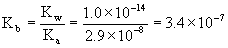 assuming 25 °C.
assuming 25 °C.
(Remember that this relationship is only true for conjugate acid–base pairs.)
(c) Use the hydrolysis reaction that generates hydroxide, write the mass action expression for the equilibrium constant, set up a table of concentrations, use this to find the pOH, and then find the pH.
OCl–(aq) + H2O(l) → ← HOCl(aq) + OH–(aq)
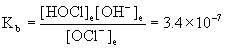
Initial 0.082 0 0
Change – x +x +x
Equilibrium 0.082 – x x x
Approximate? 0.080/3.4×10–7 = 240000 >> 100, so yes.
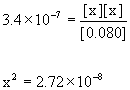
x = [OH–] = 1.6×10–4 M
pOH = –log[OH–] = –log[1.6×10–4] = 3.78
pH = 14.00 – pOH = 14.00 – 3.78 = 10.22
20. Calculate [NH4+] in a solution that is 0.15 M NH3 and 0.015 M KOH.
Write the chemical reactions (the solubility of KOH and the acid–base equilibrium for NH3), write the mass action expression for Kb (ammonia is a base), set up a table of concentrations, and solve.
KOH(aq) → K+(aq) + OH–(aq)
NH3(aq) + H2O(l) → ← NH4+(aq) + OH–(aq)
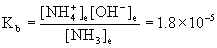
Initial 0.15 0 0.015
Change – x +x +x
Equilibrium 0.15 – x x 0.015 + x
Approximate? 0.15/1.8×10–5 = 8000 > 100, yes; 0.015/1.8×10–5 = 800 > 100, also yes.
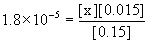
x = [NH4+] = 1.8×10–4 M
21. Predict whether an aqueous solution can be made up to have the following concentrations or whether a chemical reaction must occur.
(a) 0.25 M CH3COONa and 0.15 M HI
(b) 0.050 M KNO2 and 0.18 M KNO3
(c) 0.0050 M Ca(OH)2 and 0.0010 M HNO3
(d) 0.20 M NH4Cl and 0.35 M NaOH
(a) Write the solubilization reaction:
CH3COONa(aq) → Na+(aq) + CH3COO–(aq)
Acetate ion is basic, so will react with any acid present, so
HI(aq) + CH3COO–(aq) → CH3COOH(aq) + I–(aq)
Thus, all of the HI will be consumed and the solution cannot contain 0.15 M HI.
(b) Write the solubilization reactions:
KNO2(aq)→ K+(aq) + NO2–(aq)
KNO3(aq) → K+(aq) + NO3–(aq)
Nitrite ion is a base, but there is no acid present in solution so no further reactions occur and the given concentrations are compatible.
(c) Calcium hydroxide is a strong base and nitric acid is a strong acid, so reaction will occur
Ca(OH)2(aq) + 2 HNO3(aq) → Ca2+(aq) + 2 NO3–(aq) + 2 H2O(l)
The given concentrations are incompatible.
(d) Write the solubilization reaction:
NH4Cl(aq) → NH4+(aq) + Cl–(aq)
Ammonium ion is an acid and will react with any base present:
NH4+(aq) + NaOH(aq) → Na+(aq) + NH3(aq) + H2O(l)
The given concentrations are incompatible.
22. A solution is 0.405 M HCOOH (formic acid) and 0.326 M in the salt HCOONa (sodium formate). What is the pH of the buffer solution?
Write the dissolution reaction for sodium formate, the acid–base equilibrium for formic acid, write the mass action expression for Ka, set up a table of concentrations, and solve.
HCOONa(aq) → Na+(aq) + HCOO–(aq)
HCOOH(aq) + H2O(l) → ← H3O+(aq) + HCOO–(aq)
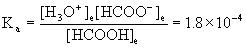
Initial 0.405 0 0.326
Change – x +x +x
Equilibrium 0.405 – x x 0.326 + x
Approximate? 0.405/1.8×10–4 = 2000 > 100, yes; 0.362/1.8×10–4 = 2000 > 100, also yes.
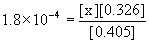
x = [H3O+] = 2.2×10–4 M
pH = –log[H3O+] = –log[2.2×10–4] = 3.66
23. Identify the Lewis acid and Lewis base in each of the following reactions.
(a) OH–(aq) + Al(OH)3(s) → Al(OH)4–(aq)
(b) Cu2+(aq) + 4 NH3(aq) → [Cu(NH3)4]2+(aq)
(c) CO2(g) + OH–(aq) → HCO3–(aq)
Lewis acids are electron pair acceptors (often cationic) and Lewis bases are electron pair donors (often anionic or have a free lone pair of electrons to donate).
(a) OH–(aq) + Al(OH)3(s) → Al(OH)4–(aq)
Lewis Acid: Al(OH)3
Lewis Base: OH–
(b) Cu2+(aq) + 4 NH3(aq) → [Cu(NH3)4]2+(aq)
Lewis Acid: Cu2+
Lewis Base: NH3
(c) CO2(g) + OH–(aq) → HCO3–(aq)
Lewis Acid: CO2
Lewis Base: OH–
24. Can a solution have [H3O+] = 2×[OH–]? Can a solution have pH = 2×pOH? If so, will the two solutions be the same?
Assume 25 °C so [H3O+][OH–] = Kw = 1.0×10–14 and pH + pOH = 14.00.
If [H3O+] = 2×[OH–], then 1.0×10–14 = [H3O+][OH–] = (2×[OH–])[OH–] = 2[OH–]2
or [OH–] = 7.1×10–8 M and [H3O+] =1.4×10–7 M. There is no reason why a solution could not have these concentrations.
If pH = 2×pOH, 14.00 = pH + pOH = 2×pOH + pOH = 3 pOH
or pOH = 4.67 and pH = 9.33. Again, these are perfectly reasonable and there is no reason why such a solution could not be prepared.
However, the two solutions are not the same. In the first case, the pH = –log[H3O+] = –log[1.4×10–7] = 6.85, which is different from the second solution having pH = 9.33.
25. Calculate the pH of a solution that is 1.0×10–8 M HCl.
Both water and HCl contribute significant amounts of hydronium ion, so both reactions must be considered. This problem, then, is a common–ion problem where HCl provides the common ion to the water autoionization equilibrium. So, write the two reactions, write the mass action expression for Kw, set up a table of concentrations, and solve. Assume 25 °C.
HCl(aq) + H2O(l) → H3O+(aq) + Cl–(aq)
H2O(l) + H2O(l) → ← H3O+(aq) + OH–(aq)
Kw = [H3O+]e[OH–]e = 1.0×10–14
Initial 1.0×10–8 0
Change +x +x
Equilibrium 1.0×10–8 + x x
1.0×10–14 = [1.0×10–8 + x][x]
1.0×10–14 = 1.0×10–8x + x2
x2 + 1.0×10–8x – 1.0×10–14 = 0
Solve with the quadratic equation to give
x = 9.5×10–8, –1.1×10–7
Only the positive value makes sense chemically, so
[H3O+] = 1.0×10–8 + x = 1.0×10–8 + 9.5×10–8 = 1.05×10–7 M
pH = –log[H3O+] = –log[1.05×10–7] = 6.979 = 6.98 (despite the sig fig rules, pH values beyond 2 decimal places are nearly always meaningless)
26. Normal rainfall is made slightly acidic from the dissolving of atmospheric CO2 in the rainwater and ionization of the resulting carbonic acid, H2CO3. At a CO2(g) partial pressure of 1 atm and a temperature of 25 °C, the solubility of CO2(g) in water is 0.759 mL CO2 at STP per mL H2O. Given that air contains 0.036% CO2 by volume, estimate the pH of rainwater that is saturated with CO2(g). (Hint: Recall Henry's law, and assume that the dissolved CO2 is present as carbonic acid.)
First, determine the molar concentration of CO2 in saturated water using Henry's law.
Change the volume solubility of CO2 in water to a molar solubility using the ideal gas law:
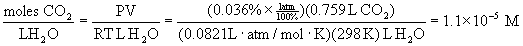
One of the assumptions in the problem is that all of the dissolved CO2 reacts with water to form carbonic acid, i.e.
CO2(aq) + H2O(l) → H2CO3(aq)
Now the problem becomes a typical weak acid equilibrium:
H2CO3(l) + H2O(l) → ← H3O+(aq) + HCO3–(aq)
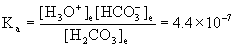
Initial 1.1×10–5 0 0
Change +x +x
Equilibrium 1.1×10–5 – x x x
Approximate? 1.1×10–5/4.4×10–7 = 25 <100, so no.
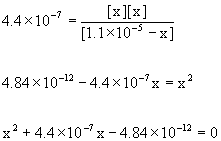
Using the quadratic equation gives
x = 2.0×10–6, –2.4×10–6
Only the positive value makes sense, so
x = [H3O+] = 2.0×10–6 M
pH = – log[H3O+] = – log[2.0×10–6] = 5.70