Practice Problems
Chemical Kinetics: Rates and Mechanisms of Chemical Reactions Practice Problems
Chemical Kinetics: Rates and Mechanisms of Chemical Reactions1. State two quantities that must be measured to establish the rate of a chemical reaction and cite several factors that affect the rate of a chemical reaction.
The rate of a reaction is defined as the change in concentration as a function of time. Thus, the two quantities that must be measured are the molarity of either a reactant or product and the time.
The factors that affect a reaction rate include the temperature, the concentration of reactants, the surface area (if solids are involved in the reaction, and the presence or absence of a catalyst.
2. Explain why the rate of disappearance of NO and the rate of formation of N2 are not the same in the reaction, 2CO(g) + 2NO(g) → 2CO2(g) + N2(g).
Because of the 2:1 stoichiometric ratio between NO and N2, the NO must use 2 moles for each mole of N2 produced. This means that the rate of consumption of NO is twice as fast as the rate of production of N2.
3. What plot of experimental data can be used to evaluate the activation energy, Ea, of a reaction? How is Ea related to this plot?
The experimental data required to evaluate the activation energy are rate constants as a function of absolute temperature. If ln k is plotted against 1/T, a straight line should result and the slope of the line is equal to –Ea/R, where R is the ideal gas constant in energy units.
4. What are the chief requirements that must be met by a plausible reaction mechanism? Why do we say "plausible" mechanism rather than "correct" mechanism?
A reaction mechanism must meet two criteria. 1) The sum of all of the steps in the mechanism must match the observed reaction, i.e., the stoichiometry of the reaction must be satisfied. 2) The reaction mechanism must account for the experimentally observed rate law.
Reaction mechanisms are considered "plausible" rather than "correct" because different sequences of elementary reactions may meet the two requirements.
5. In a reaction mechanism, (a) what is the difference between an activated complex and an intermediate? (b) What is meant by the rate-determining step? Which elementary reaction in a reaction mechanism is often the rate-determining step?
(a) An activated complex is the structure along the reaction pathway of the highest energy, which determines the activation energy for the reaction. An intermediate can be any structure found in the reaction path.
(b) The rate-determining step is the elementary reaction that controls the mathematical form of the overall rate law. The rate-determining step is usually the slowest elementary reaction.
6. In the reaction H2O2(aq) → H2O(l) + ½ O2(g), the initial concentration of H2O2 is 0.2546 M, and the initial rate of reaction is 9.32×10–4 M s–1. What will be [H2O2] at t = 35 s?
Use the definition of rate (change in concentration over change in time), recognizing that the initial rate for the loss of hydrogen peroxide is negative and at t = 0 s, [H2O2] = 0.2546 M.
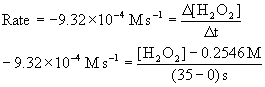
[H2O2] = 0.2220 M
7. For the reaction, A → products, a graph of [A] versus time is a curve. What can be concluded about the order of this reaction?
The integrated rate laws, written as linear equations, are:
For zero order reactions: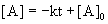 
For first order reactions: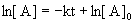 
For second order reactions: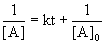 
Since [A] vs. t is a curve, the reaction can not be zero order.
8. Following are two statements pertaining to the reaction 2A + B → 2C, for which the rate law is rate = k[A][B]. Identify which statement is true and which is false, and explain your reasoning.
(a) The value of k is independent of the initial concentrations [A]0 and [B]0.
(b) The unit of the rate constant for this reaction can be expressed either as s–1 or min–1.
The rate law is second order overall. The rate constant, by definition, is independent of concentrations, initial or otherwise, so (a) must be true. The units of the rate constant for a second order reaction are M–1s–1 or M–1min–1 (rate = Ms–1 = k[M][M]) so (b) is false.
9. The rate of the following reaction in aqueous solution is monitored by measuring the number of moles of Hg2Cl2 that precipitate per liter per minute. The data obtained are listed in the table.
2 HgCl2(aq) + C2O42–(aq) → 2 Cl–(aq) + 2 CO2(g) + Hg2Cl2(s)
Experiment [HgCl2] (M) [C2O42–] (M) Initial rate (mol L–1 min–1)
1 0.105 0.15 1.8×10–5
2 0.105 0.15 1.8×10–5
3 0.052 0.30 7.1×10–5
4 0.052 0.15 8.9×10–6
(a) Determine the order of reaction with respect to HgCl2, with respect to C2O42– and overall.
(b) What is the value of the rate constant k?
(c) What would be the initial rate of reaction if [HgCl2] = 0.094 M and [C2O42–] = 0.19 M?
(d) Are all four experiments necessary to answer parts (a) - (c)? Explain.
Use the method of initial rates to find the orders of reaction in each component. This will allow evaluation of the rate constant and the initial rate of reaction at any other condition.
(a) Rate = k[HgCl2]m[C2O42–]n
Compare the rates in experiments 1 and 2 (or 3 and 4) to find the order in oxalate ion:
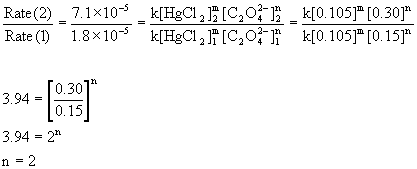
Compare the rates in experiments 2 and 3 (or 1 and 4) to find the order in mercury(II) chloride:
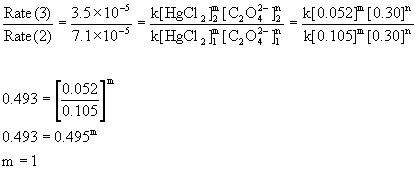
Therefore, the reaction is first order with respect to mercury(II) chloride and second order with respect to oxalate. The overall order is the sum of these, 2 + 1 = 3, third order.
(b) To find the rate constant, use the rate equation and solve for k:
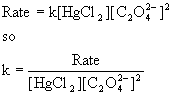
Experiment [HgCl2] (M) [C2O42–] (M) Initial rate (mol L–1 min–1) k
1
0.105
0.15
1.8×10–5
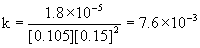
2
0.105
0.15
1.8×10–5
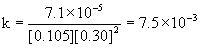
3
0.052
0.30
7.1×10–5
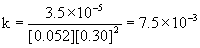
4
0.052
0.15
8.9×10–6
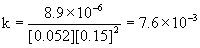
The average k = 7.6×10–3 M–2min–1
(c) Rate = k[HgCl2][C2O42–]2
Rate = (7.6×10–3 M–2min–1)[0.094 M][0.19 M]2 = 2.6×10–5 M min–1
(d) Since there are only two reactants, three experiments are the minimum required to find the rate equation and rate constant. Experiments 1 - 3 would have sufficed to answer the questions posed.
10. In the reaction A → products, we find that when [A] has fallen to half of its initial value, the reaction proceeds at the same rate as its initial rate. Is the reaction zero order, first order, or second order? Explain.
Since the rate is not changing as a function of time, the reaction must be zero order.
11. In the reaction, A → products, with the initial concentration [A]0 = 1.512 M, [A] is found to be 1.496 M at t = 30 s. With the initial concentration [A]0 = 2.584 M, [A] is found to be 2.552 M at t = 1 min. What is the order of this reaction?
First, find the rate of reaction in each experiment, being sure to be consistent in units. Then use the Method of Initial rates to find the order of reaction.
Experiment [A]0 (M) [A] (M) at t (s) Rate (M s–1)
1
1.512
1.496 at 30 s
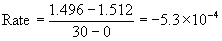
2
2.584<
2.552 at 60 s
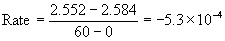
Since the rates are the same for both experiments, the reaction must be zero order. Mathematically:
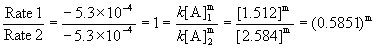, which can only be true for m = 0.
12. A first order reaction, A → products, has a rate of reaction of 0.00250 M s–1 when [A] = 0.484 M. (a) What is the rate constant, k, for this reaction? (b) Does t3/4 depend on the initial concentration? Does t4/5? Explain.
(a) For a first order reaction, Rate = k[A]. Since the rate and concentration are known, solving the equation for k gives the required answer.
k = Rate/[A] = 0.00250 M s–1/0.0484 M = 5.17×10–3 s–1.
(b) Neither t3/4 nor t4/5 depend upon intial concentration because this is a first order reaction, which means that the time associated reaction is simply related to the rate constant.
13. In the first-order decomposition of dinitrogen pentoxide at 335 K,
N2O5(g) → 2 NO2(g) + ½ O2(g)
if we start with a 2.50-g sample of N2O5 at 335 K and have 1.50 g remaining after 109 s, (a) What is the value of the rate constant k? (b) What is the half-life of the reaction? (c) What mass of N2O5 will remain after 5.0 min?
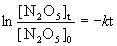
Since the concentration units cancel out, we can work directly in grams for this problem.
(a) [N2O5]0 = 2.50 g, [N2O5]t = 1.50 g, t = 109 s, so
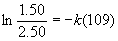
so k = 4.69×10–3 s–1
(b) t½ = 0.693/k = 0.693/4.69×10–3 = 148 s.
(c) t = 5.0 min = 300. s, so
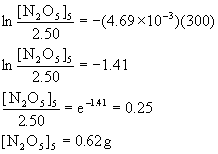
14. The smog constituent peroxyacetyl nitrate (PAN) dissociates into peroxyacetyl radicals and NO2(g) in a first order reaction with a half-life of 32 min.
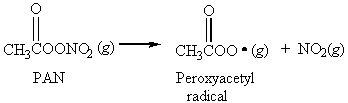
If the initial concentration of PAN in an air sample is 2.7×1015 molecules/L, what will be the concentration 2.24 h later?
For a first order reaction, the integrated rate law is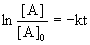 
and the rate constant can be found from the half-life: 
.
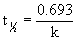Thus, k = 0.693/t½ = 0.693/32 = 0.022 min–1. For an initial concentration [PAN]0 = 2.7 ×1015 molecules/L and at t = 2.24 h = 134 min:
[PAN] = [PAN]oe–kt = (2.7×1015)e–(0.022)(134) = 1.4×1014 molecules/L.
15. The following data were obtained in two separate experiments in the reaction: A → products. Determine the rate law for this reaction, including the value of k.
Experiment 1 Experiment 2
[A] (M) time (s) [A] (M) time (s)
0.800 0 0.400 0
0.775 40 0.390 64
0.750 83 0.380 132
0.725 129 0.370 203
0.700 179 0.360 278
The general rate law is Rate = –k[A]m; the method of initial rates can be used to establish the order of reaction and give an estimate of the rate constant.
The initial rate are found from the first two data points in each experiment:
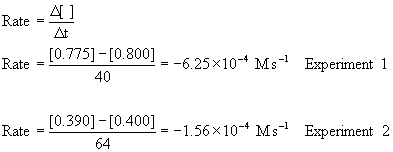
Using the initial concentrations with the initial rates:
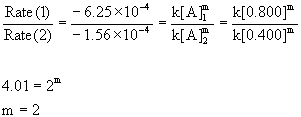
So this is a second order reaction. The rate constant can estimated from k = –Rate/[A]2 for each experiment: k(exp. 1) = –(–6.25×10–4)/[0.800]2 = 9.8×10–4 M–1 s–1 and k(exp. 2) = –(–1.56×10–4)/[0.400]2 = 9.8×10–4 M–1 s–1.
k = 9.8×10–4 M–1 s–1
To confirm this and get a better value for the rate constant, a plot of [A]–1 vs. t should be linear with a slope equal to the rate constant:
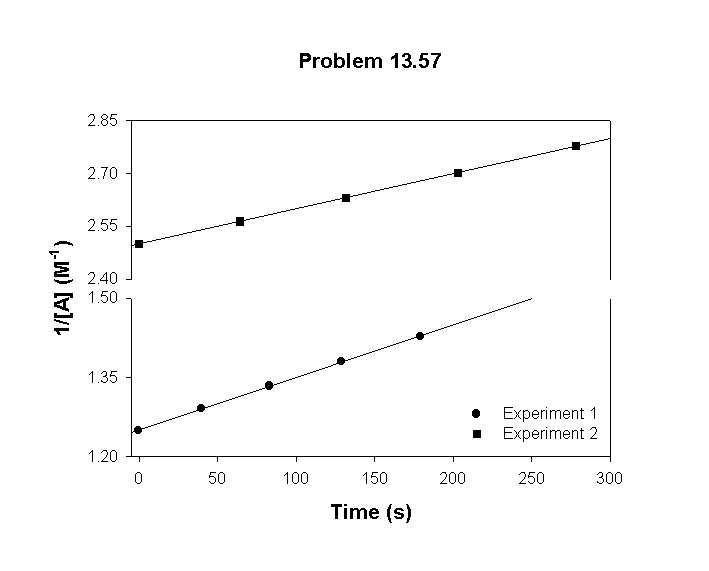
The slopes of these plots show that a better value for the rate constant is k = 1.0×10–3 M–1 s–1.
16. Listed below are initial rates, expressed in terms of the rate of decrease of partial pressure of a reactant for the following reaction at 826 °C. Determine the rate law for this reaction, including the value for k.
NO(g) + H2(g) → ½N2(g) + H2O(g)
With initial PH2 = 400 mmHg With initial PNO = 400 mmHg
Initial PNO (mmHg) Rate (mmHg/s) Initial PH2 (mmHg) Rate (mmHg/s)
359 0.750 289 0.800
300 0.515 205 0.550
152 0.125 147 0.395
The unknown rate law is given by Rate = k[NO]m[H2]n. Using the Method of Initial rates will give the rate law and the value of the rate constant. Since the units cancel in the Method of Initial rates, we do not need to convert to molarity.
To find the order in NO, use the first set of data where the pressure of H2 is kept constant. Experiments 2 and 3 are about a factor of 2 difference in initial pressure of NO, so will give easier numbers to work with:
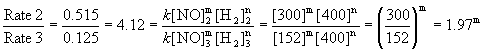
Within experimental error, m = 2, or second order in NO.
To find the order in H2, use experiments 1 and 3 for the easiest numbers:
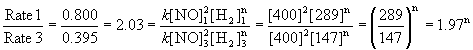
Within experimental error, n = 1, or first order in H2.
The rate constant can now be found from the rate law: k = Rate/[NO]2[H2] for each experiment:
Initial PH2 (mmHg) Initial PNO (mmHg) Initial Rate (mmHg/s) k (mmHg–2 s–1)
400 359 0.750 (0.750)/(400)(359)2 = 1.45×10–8
400 300 0.515 (0.515)/(400)(300)2 = 1.43×10–8
400 152 0.125 (0.125)/(400)(152)2 = 1.35×10–8
289 400 0.800 (0.800)/(289)(400)2 = 1.73×10–8
205 400 0.550 (0.550)/(205)(400)2 = 1.68×10–8
147 400 0.395 (0.395)/(147)(400)2 = 1.68×10–8
Averaging all of the k values gives k = 1.55×10–8 mmHg–2 s–1
17. Rate constants for the first-order decomposition of acetonedicarboxylic acid
CO(CH2COOH)2(aq) → CO(CH3)2(aq) + 2 CO2(g)
acetonedicarboxylic acidacetone
are k = 4.75 ×10–4 s–1 at 293 K and k = 1.63 ×10–3 at 303 K. What is the activation energy, Ea, for this reaction?
Use the two-point form of the Arrhenius equation to answer this question:
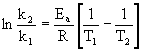
where k2 = 1.63 ×10–3 at T2 = 303 K and k1 = 4.75 ×10–4 at T1 = 293 K.
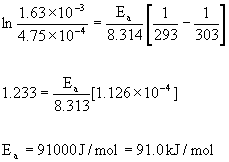
18. The following is proposed as a plausible reaction mechanism:
A + B → I(slow)
I + B → C + D(fast)
What is (a) the net reaction described by this mechanism and (b) a plausible rate law for the reaction?
(a) To find the net reaction, sum up all the reactions in the mechanism and eliminate common species on each side of the equation:
A + B + I + B → I + C + D
net: A + 2B → C + D
(b) The rate law is determined by the slow step in the reaction mechanism. Since a reaction mechanism is composed of elementary reactions, the rate law for the slow step can be written by inspection, with the orders of reaction being the stoichiometric coefficients:
Rate = k[A][B]
19. The following reaction exhibits the rate law: Rate = k[NO]2[Cl2].
2 NO(g) + Cl2(g) → 2 NOCl(g)
Explain why the following mechanism is not plausible for this reaction.
NO(g) + Cl2 → ← NOCl(g) + Cl(g)fast
NO(g) + Cl(g) → NOCl(g)slow
The rate law is determined by the slow step: Rate = kslow[NO][Cl]
However, this rate law includes and intermediate that cannot be part of the rate law for the overall reaction - only NO or Cl2 can be part of the rate law. The [Cl] term can be eliminated using the fast, reversible step where the rate of the forward reaction is the same as the rate of the reverse reaction:
Rateforward = Ratereverse
Rateforward = kforward[NO][Cl2]
Ratereverse = kreverse[NOCl][Cl]
so kforward[NO][Cl2] = kreverse[NOCl][Cl]
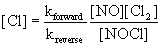
substituting for [Cl] in the slow step rate law gives:
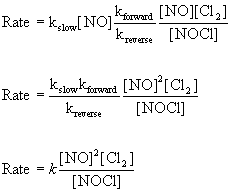
This rate does not match the experimental rate law so this cannot be a plausible mechanism.
20. Show that the proposed mechanism is consistent with the rate law for the following reaction in aqueous solution,
Hg22+(aq) + Tl3+(aq) → 2 Hg2+(aq) + Tl+(aq)
for which the observed rate law is
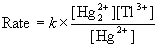
Proposed Mechanism:
Hg22+(aq) → ← Hg2+(aq) + Hg(s)fast
Hg(s) + Tl3+(aq) → Hg2+(aq) + Tl+(aq) slow
First, check to see that the proposed mechanism matches the experimental stoichiometry.
Add the two reactions together to give:
Hg22+(aq) + Hg(s) + Tl3+(aq) → Hg2+(aq) + Hg(s) + Hg2+(aq) + Tl+(aq)
The Hg(s) common to both sides of the equation cancel out and the two moles of Hg2+(aq) can be collected to give the observed reaction, so the stoichiometry matches.
The proposed mechanism can be rewritten as
Hg22+(aq) → k1 Hg2+(aq) + Hg(s) Rate = k1[Hg22+] (fast)
Hg2+(aq) + Hg(s) → k–1 Hg22+(aq) Rate = k–1[Hg2+][Hg] (fast)
Hg(s) + Tl3+(aq) → k2 Hg2+(aq) + Tl+(aq) Rate = k2[Hg2+][Hg] (slow)
The overall rate is determined by the slow step, but this has an intermediate ([Hg}) that must be eliminated in order to evaluate the mechanism. This can be done using the two fast steps, which must have approximately the same rate, or:
k1[Hg22+] = k–1[Hg2+][Hg]
so
[Hg] = k1[Hg22+]/k–1[Hg2+]
Using this expression in the rate law for the slow step gives
Rate = k2[Hg2+] k1[Hg22+]/ k–1[Hg2+]
or
Rate = (k2k1/k–1)[Hg2+ [Hg22+]/[Hg2+]
which exactly matches the observed rate law when k = k2k1/k–1
21. Benzenediazonium chloride decomposes in water yielding N2(g).
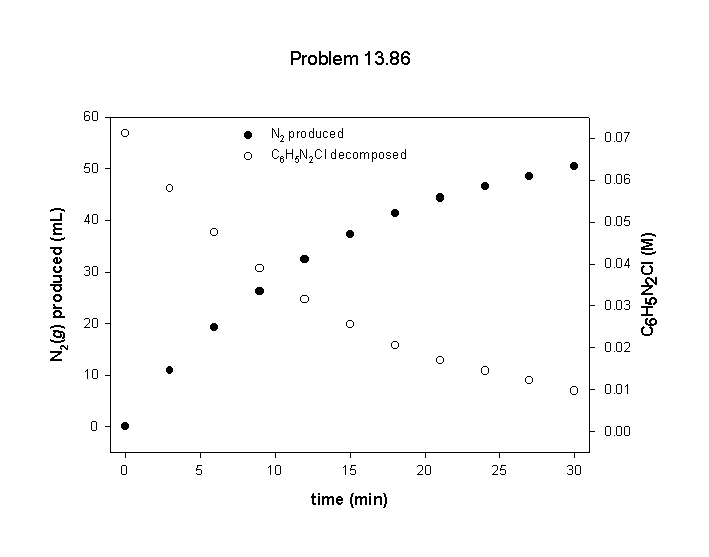
C6H5N2Cl(aq) → C6H5Cl(aq) + N2(g)
The data tabulated below were obtained for the decomposition of a 0.071 M solution at 50 °C (t = ∞ corresponds to the completed reaction). To obtain [C6H5N2Cl] as a function of time, note that during the first 3 min, the volume of N2(g) produced was 10.8 mL of a total of 58.3 mL, corresponding to this fraction of the total reaction: 10.8 mL/58.3 mL = 0.185. An equal fraction of the available C6H5N2Cl was consumed during the same time.
time (min)N2(g) (mL)
00
310.8
619.3
926.3
1232.4
1537.3
1841.3
2144.3
2446.5
2748.4
3050.4
∞58.3
(a) Plot graphs showing the disappearance of C6H5N2Cl and the formation of N2(g) as a function of time.
(b) What is the initial rate of formation of N2(g)?
(c) What is the rate of disappearance of C6H5N2Cl at t = 20 min?
(d) What is the half-life, t½, of the reaction?
(e) Write the rate law for this reaction, including a value for k.
(a) First, find the concentrations of C6H5N2Cl remaining at each time:
time (min)N2(g) (mL) fraction N2 = mL/58.3 mL C6H5N2Cl (M) = 0.071×(1 – fraction)
00 0/58.3 = 0.00 0.071(1 – 0) = 0.071
310.8 10.8/58.3 = 0.185 0.071(1 – 0.185) = 0.058
619.3 19.3/58.3 = 0.331 0.071(1 – 0.331) = 0.047
926.3 26.3/58.3 = 0.451 0.071(1 – 0.451) = 0.039
1232.4 32.4/58.3 = 0.556 0.071(1 – 0.556) = 0.032
1537.3 37.3/58.3 = 0.640 0.071(1 – 0.640) = 0.026
1841.3 41.3/58.3 = 0.708 0.071(1 – 0.708) = 0.021
2144.3 44.3/58.3 = 0.760 0.071(1 – 0.760) = 0.017
2446.5 46.5/58.3 = 0.798 0.071(1 – 0.798) = 0.014
2748.4 48.4/58.3 = 0.830 0.071(1 – 0.830) = 0.012
3050.4 50.4/58.3 = 0.864 0.071(1 – 0.864) = 0.0097
∞58.3 58.3/58.3 = 1.00 0.071(1 – 1.00) = 0.00
The plots are:
(b) From the definition of rate,
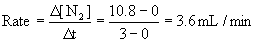
(c) Again, using the definition of rate and approximating t = 20 min using the t = 18 min and t = 21 min points,
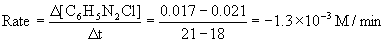
(d) The initial concentration of benzenediazonium chloride is 0.071 M, so the first half-life is reached when the concentration has reached 0.0355 M. Using the graph from part (a) gives t½ ~ 10 min.
(e) The order of the reaction can be determined by looking at the time of the second half-life, when the benzenediazonium chloride concentration has been reduced to ½ of its initial value, 0.018 M. This occurs at ~21 min, just twice the time for the first half-life. Since t½ is the same for the two different time intervals, this means that the reaction is first order.
Rate = k[C6H5N2Cl]
Plotting ln[C6H5N2Cl] vs. t confirms this and the slope of the plot gives the rate constant, k.
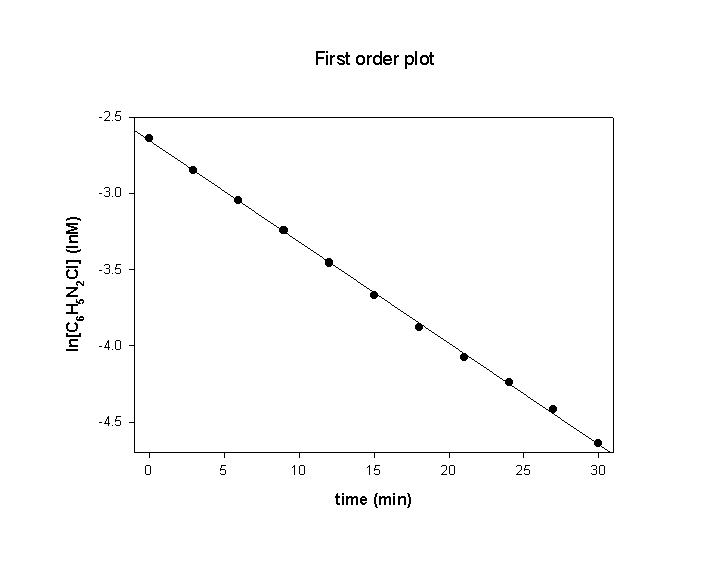
The slope of the plot = –0.0664, so k = 0.0664 min–1. (This allows a better estimate of the half-life to be t½ = 0.693/k = 0.693/0.0664 = 10.4 min.)
22. Hydroxide ion is involved in the mechanism but not consumed in this reaction in aqueous solution.
OCl–(aq) + I–(aq) → OH– OI–(aq) + Cl–(aq)
(a) From the data in the table, determine the order of reaction with respect to OCl–, I–, and OH–, and the overall order.
[OCl–] (M)[I–] (M) [OH–] (M) Rate of formation of OI– (mol L–1 s–1)
0.00400.0020 1.00 4.8×10–4
0.00200.0040 1.00 5.0×10–4
0.00200.0020 1.00 2.4×10–4
0.00200.0020 0.50 4.6×10–4
0.00200.0020 0.25 9.4×10–4
(b) Write the rate law, and determine the value of the rate constant, k.
(c) Show that the following mechanism is consistent with the net equation and with the rate law. Which is the rate–determining step?
OCl –(aq) + H2O(l) → ← HOCl(aq) + OH –(aq)
I –(aq) + HOCl(aq) → HOI(aq) + Cl –(aq)
HOI(aq) + OH –(aq) → H2O(l) + OI –(aq)
(d) Is it appropriate to refer to OH–as a catalyst in this reaction? Explain.
(a) Use the method of initial rates for a rate law of the general form Rate = k[OCl–]m[I–]n[OH–]p. Experiments 1 and 3 give the order in hypochlorite ion (iodide and hydroxide are constant): doubling the concentration of hypochlorite doubles the initial rate, meaning that the reaction is 1st order in hypochlorite ion, m = 1. Experiments 2 and 3 can be used to find the order in iodide ion (hypochlorite and hydroxide are unchanged): doubling the iodide concentration doubles the rate so the reaction is also first order in iodide ion, n = 1. Experiments 3 and 4 can be used to find the order in hydroxide (hypochlorite and iodide are unchanged): doubling the concentration halves the rate, so the order in hydroxide must be –1, p = –1. Mathematically:
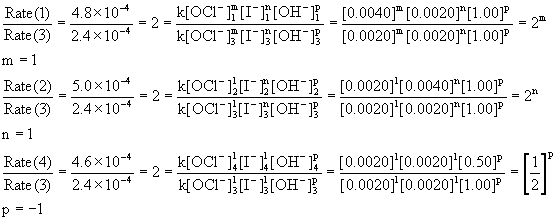
The overall order is the sum of each individual order = 1 + 1 + –1 = 1
(b) Based on the orders found above, the rate law is:
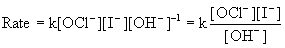
The rate constant can be found by using the rate law and the data:
[OCl–] (M)[I–] (M) [OH–] (M) Rate of formation of OI– (mol L–1 s–1)
0.00400.0020 1.00 4.8×10–4 60.0 s–1
0.00200.0040 1.00 5.0×10–4 62.5 s–1
0.00200.0020 1.00 2.4×10–4 60.0 s–1
0.00200.0020 0.50 4.6×10–4 57.5 s–1
0.00200.0020 0.25 9.4×10–4 58.75 s–1
The average rate constant (to the correct number of significant figures) = 60. s–1
(c) First, add all the equations in the mechanism together to see if the stoichiometry of the mechanism is correct:
OCl–(aq) + H2O(l) + I–(aq) + HOCl(aq) + HOI(aq) + OH–(aq) → HOCl(aq) + OH–(aq) + HOI(aq) + Cl–(aq) + H2O(l) + OI–(aq)
After eliminating common species:
OCl–(aq) + I–(aq) → OI–(aq) + Cl–(aq)
which is the correct stoichiometry.
To find the rate–determining step, consider the rate law for each elementary reaction:
Step 1, forward reaction: Rate = kforward[OCl–][H2O]
Step 1, reverse reaction: Rate = kreverse[HOCl][ OH–]
Step 2: Rate = k2[I–][HOCl]
Step 3: Rate = k3[HOI][OH–]
Step 1, forward does not have enough terms in the rate law. Step 1, reverse and Step 3 both have hydroxide in the numerator but the experimental rate law requires it to be in the denominator. This leaves Step 2 as the likely slow step, but this has an intermediate that must be eliminated by using Step 1, assuming it to be a fast step:
For Step 1, Rateforward = Ratereverse so kforward[OCl–][H2O] = kreverse[HOCl][OH–]
Solving for the intermediate, [HOCl] gives:
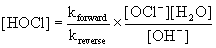
Substituting this into the rate law for Step 2, the proposed slow step, gives:
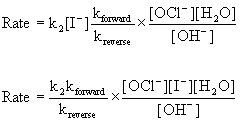
Since water is the solvent, its concentration does not change and should be grouped with the constants:
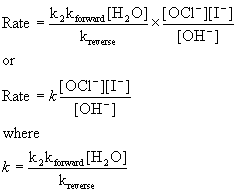
This now matches the experimental rate law.
(d) Since hydroxide is found in the denominator of the rate law, an increase in concentration slows the reaction down so OH– is an inhibitor, not a catalyst. Compare experiments 3, 4, and 5 to see how decreasing the hydroxide increases the reaction rate.
